что означает буква b в названии b tree index
Повесть о кластеризованном индексе
После перехода на SQL Server с Oracle удивляет многое. Трудно привыкнуть к автоматическим транзакциям – после update не нужно набирать commit (что приятно), зато в случае ошибки не сможешь набрать rollback (что просто кошмарно). Трудно привыкнуть к архитектуре, в которой журнал используется и для отката, и для наката транзакций. Трудно привыкнуть к ситуации «писатель блокирует читателей, читатель блокирует писателей», а когда привыкнешь – ещё труднее отвыкнуть. И совсем не последнее место в рейтинге трудностей играет засилье кластеризованных индексов. По умолчанию первичный ключ таблицы – именно кластеризованный индекс, и поэтому почти у всех таблиц он есть.
На самом деле зверь этот совсем нестрашный и даже очень полезный. Давайте попробуем разобраться, зачем он нужен и как его использовать.
Файлы, страницы, RID
Данные любой таблицы физически сохранены в файле базы данных. Файл БД делится на страницы (page) – логические единицы хранения для сервера. Страница в MS SQL Server обязательно имеет размер 8 килобайт (8192 байта), из них под данные отдано 8060 байт. Для каждой строки можно указать её физический адрес, так называемый Row ID (RID): в каком файле она находится, в какой по порядку странице этого файла, в каком месте страницы. Страницу таблица присваивает целиком – на одной странице могут быть данные только одной таблицы. Более того, при необходимости считать/записать строку сервер считывает/записывает всю страницу, поскольку так получается гораздо быстрее.
Как устроен B-tree индекс?
B-tree означает balanced tree, «сбалансированное дерево». Индекс содержит ровно одну корневую страницу, которая является точкой входа для поиска. Корневая страница содержит значения ключей и ссылки на страницы следующего уровня для данных значений индекса. При поиске по индексу находится последнее значение, которое не превосходит искомое, и происходит переход на соответствующую страницу. На последнем, листьевом уровне дерева перечислены все ключи, и для каждого из них указана ссылка (bookmark) на данные таблицы. Естественным кандидатом на роль ссылки является RID, и он в самом деле используется в этом качестве для случая кучи. На следующем рисунке буквы B обозначают ссылки на строки таблицы.
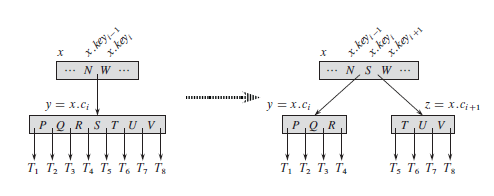
При добавлении записи в таблицу её необходимо также добавить в индекс. Новая запись индекса, ссылающаяся на запись таблицы, вставляется в страницу листьевого уровня. При этом может оказаться, что на этой странице нет свободного места. Тогда:
Понятно, что добавление записей в таблицу при наличии индекса становится заметно более дорогостоящим процессом – каждое разбиение страницы требует обновления как минимум 4 страниц (разделяемую, следующую за разделяемой, новую, родительскую).
При этом наличие индекса резко ускоряет поиск данных: вместо сплошного сканирования можно вести двоичный поиск, спускаясь по дереву. Также за счёт наличия горизонтальных ссылок на страницы одного уровня пройти диапазон ключей индекса можно очень быстро. И мы плавно подходим к основным задачам выборки: поиск одного значения и сканирование диапазонов.
Куча мала
Рассмотрим некоторую модельную таблицу, организованную в виде кучи: какого-то определённого порядка в записях нет.
RID, который запись получает в самом начале, остаётся с ней почти всегда. В редких случаях записи в куче могут перемещаться на другую страницу – это происходит, когда после обновления строка перестаёт помещаться на то место, которое она занимала. Но в таком случае на прежнем месте остаётся ссылка на новое размещение – то есть, зная RID, полученный строкой при добавлении, строку можно найти всегда. Поэтому для индексов на куче наилучший выбор для ссылки на данные – именно RID.
Предположим, в таблице 200 тысяч записей, и в каждую страницу помещается от 48 до 52 записей. Будем считать, что таблица занимает 4000 страниц. Допустим, нам нужно найти все записи, в которых поле [City] имеет значение ‘Perm’. Также допустим, что их всего 3, но мы об этом пока не знаем.
Серверу придётся просканировать все 4000 страниц. Даже если сервер найдёт все 3 записи, ему всё равно придётся идти до конца – ведь нет гарантии, что больше нужных записей нет. Итак, для выполнения запроса понадобится 4000 логических чтений страницы.
А если у нас есть индекс, в котором можно искать двоичным поиском – скажем, дерево высоты 3? Тогда серверу потребуется 3 чтения индексных страниц для того, чтобы найти адрес первой записи. Адреса второй и третьей записей будут лежать рядом – либо в той же странице, либо в следующей: страницы индекса по горизонтали соединены ссылками. То есть после максимум 4 чтений сервер наверняка знает RID всех трёх записей. Если сильно не повезёт, все 3 записи лежат в разных страницах. Таким образом, при наличии индекса после 7 логических чтений страницы все 3 записи наверняка будут найдены. 7 против 4000 – впечатляет.
Но так хорошо будет, когда записей мало. А если это не ‘Perm’, а ‘Moscow’, и нужных записей не 3, а 20 тысяч? Это не очень много, всего 10 процентов от общего количества записей. Но картина быстро становится не столь радужной.
За 3 чтения сервер найдёт первую запись. А затем ему потребуется считать 20 тысяч RID и 20 тысяч раз прочитать страницу, чтобы получить строку: мы помним, что сервер читает данные только целыми страницами. Вполне может получиться так, что нужные записи рассеяны по всей таблице, и для обеспечения 20 тысяч логических чтений потребуется считать большую часть страниц с диска. Ещё хорошо, если не все. Вместо 4 тысяч логических чтений мы получаем 20 тысяч.
Индекс очень хорошо работает на поиске небольшого количества значений, но плохо работает на прохождении больших диапазонов.
Оптимизатор запросов прекрасно осведомлён об этом. Поэтому если он ожидает, что поиск по индексу даст достаточно большой диапазон, вместо поиска по индексу он выберет полное сканирование таблицы. Это, кстати, одно из редких мест, где Оптимизатор может ошибиться, даже имея правильные статистики. Если на самом деле требуемые данные расположены очень компактно (например, 20 тысяч логических чтений – это 60 раз прочесть блок с диска и 19940 раз прочесть блок в кэше), то принудительное использование индекса даст выигрыш в памяти и в скорости.
А как же быть с диапазонами?
Проблема именно в том, что в конце поиска по индексу сервер получает не данные, а только адрес, по которому они лежат. Серверу ещё нужно идти по этому адресу и брать данные оттуда. Вот было бы здорово, если бы в конце пути сразу лежали данные!
Некоторые, собственно, и лежат. Значения ключей, например, лежат именно в индексе – за ними идти не нужно. Только за неключевыми полями. А что будет, если неключевые поля тоже положить в индекс? Ну допустим, не все, а только те, которые нужны сканирующему запросу?
А будет в таком случае индекс с добавочными (included) столбцами. Он проигрывает обычному индексу по размеру: его листьевые страницы содержат не только ключи и адреса строк, но и часть данных. В поиске одиночного значения такой индекс работает не хуже, а в сканировании диапазонов – намного, намного лучше. Если индекс покрывает запрос (то есть содержит все столбцы, перечисленные в запросе), то для выполнения запроса таблица не нужна вообще. Возможность взять все требуемые данные из индекса, не обращаясь к закладкам, даёт громадный выигрыш.
Вернёмся к нашему модельному примеру. Предположим, что требуемые для запроса столбцы включены в индекс. Для простоты предположим, что в листьевую страницу индекса попадают ровно 50 записей (ключи, добавленные столбцы, ссылки на записи). Тогда сканирование 20 тысяч записей потребует чтения всего лишь 400 страниц индекса – вместо 20 тысяч логических чтений для непокрывающего индекса.
400 против 20 тысяч – разница в 50 раз. Оптимизатор запросов недаром любит предлагать включить в индекс те или иные столбцы.
А может, стоит добавить в индекс все столбцы? Тогда любой запрос будет покрыт индексом обязательно. Более того, тогда в листьях даже не нужны RID, потому что ни за какими данными такой индекс не будет обращаться в таблицу, у него всё под рукой. Да в таком случае становится не нужна и сама таблица!
И мы пришли к концепции кластеризованного индекса. Он устроен как обычное B-дерево, но в его листьевых страницах вместо ссылок на записи таблицы расположены сами данные, а отдельной от него таблицы больше нет. Таблица не может иметь кластеризованный индекс, она может быть кластеризованным индексом.
Любое сканирование по ключу в кластеризованном индексе будет лучше, чем полный просмотр таблицы. Даже если просканировать нужно 97% всех записей.
Где подвох?
Первый – понятно где. Кластеризованный индекс – это таблица, а таблица может быть только одна. Сервер должен иметь мастер-копию данных, и только из одного индекса он готов выбросить все закладки и оставить только сами данные. Если есть ещё один индекс, в который включены все поля – в нём всё равно будут и адреса строк.
Есть и второй подвох. При наличии кластеризованного индекса в качестве адреса строки уже нельзя использовать RID. Записи в кластеризованном индексе отсортированы (физически – в пределах страницы, логически – горизонтальными ссылками между страницами). При добавлении записи или изменении ключевых полей запись перемещается в правильное место – часто в пределах страницы, но возможно и перемещение на другую страницу. Иными словами, RID в кластеризованном индексе перестаёт идентифицировать запись однозначно. Поэтому в качестве адреса строки, однозначно её идентифицирующего, используется ключ кластеризованного индекса.
То есть при поиске в некластеризованном индексе после прохода по его дереву мы получаем не адрес данных, а ключ кластеризованного индекса. Для получения самих данных нужно пройти дерево кластеризованного индекса тоже.
Представим себе сканирование диапазона в 20 тысяч записей по некластеризованному индексу, построенному на кластеризованном. Теперь понадобится выполнить не 20 тысяч логических чтений страницы по известному RID, а 20 тысяч поисков в кластеризованном индексе – и каждый поиск потребует 3, а то и более, логических чтений.
А если ключ кластеризованного индекса не уникален? А так не бывает. Для сервера он обязательно уникален. Если пользователь попросил создать неуникальный кластеризованный индекс, сервер к каждому ключу припишет 4-байтовое целое число, которое обеспечит уникальность ключа. Делается это прозрачно для пользователей: сервер не только не сообщает им точного значения числа, но и не выдаёт сам факт его наличия. Уникальность ключа нужна именно для возможности однозначной идентификации записей – чтобы ключ кластеризованного индекса мог служить адресом строки.
Так делать или не делать?
Вооружённые теорией, мы можем описать рациональную процедуру построения кластеризованного индекса. Следует выписать все индексы, которые нужны таблице, и выбрать из них кандидата на кластеризацию.
Не нужно делать кластеризованный индекс только для того, чтобы он был. Если по ключу индекса не предполагается сканирование – это не очень хороший кандидат для кластеризации (если по другим индексам сканирование предполагается – то даже очень плохой кандидат). Неправильный выбор кандидата на кластеризацию ухудшит производительность, потому что все остальные индексы станут работать хуже, чем работали на куче.
Предлагается следующий алгоритм выбора:
Постскриптум. Почему он единственный?
Когда я начинал писать эту статью – я прекрасно понимал, почему у таблицы не может быть больше одного кластеризованного индекса. В середине написания я понимать это перестал и теперь уже не понимаю (хотя, что смешно, по-прежнему могу это объяснить). Сейчас у меня есть только гипотезы.
Кластеризованный индекс, во-первых, содержит все данные в листьевых вершинах, а во-вторых, не содержит никаких ссылок на данные таблицы (потому что никакой внешней по отношению к нему таблицы нет). Ну и что мешает завести несколько так устроенных индексов – содержащих все поля и не содержащих ссылки? Я не знаю. Могу только предложить.
Прежде всего – мы же можем завести сколько угодно индексов, в которые будут включены все поля. Значит, весь выигрыш, который нам сулит наличие нескольких кластеризованных индексов, относительно невелик: на листьевом уровне добавочных индексов не будет ссылок на данные, то есть мы сэкономим немного места. А какие проблемы повлечёт за собой создание нескольких кластеризованных индексов?
Сейчас я склоняюсь к мысли, что запрет множественных кластеризованных индексов связан с тем, что реализация этой концепции затратна и чревата ошибками (то есть понижением надёжности), а выгод принесла бы относительно мало. Иными словами, сделать несколько кластеризованных индексов технически можно, но дорого, неудобно и ни к чему.
Возможно, что я не вижу какие-нибудь соображения, вследствие которого делать несколько кластеризованных индексов нельзя. Буду очень признателен, если кто-то укажет мне эти соображения.
«Под капотом» индексов Postgres

Капитан Немо у штурвала «Наутилуса»
Индексы — один из самых мощных инструментов в реляционных базах данных. Мы используем их, когда нужно быстро найти какие-то значения, когда объединяем базы данных, когда нужно ускорить работу SQL-операторов и т.д. Но что представляют собой индексы? И как они помогают ускорять поиск по БД? Для ответа на эти вопросы я изучил исходный код PostgreSQL, отследив, как происходит поиск индекса для простого строкового значения. Я ожидал найти сложные алгоритмы и эффективные структуры данных. И нашёл.
Здесь я расскажу о том, как устроены индексы и как они работают. Однако я не ожидал, что в их основе лежит информатика. В понимании подноготной индексов также помогли комментарии в коде, объясняющие не только как работает Postgres, но и почему он так работает.
Поиск последовательностей
Алгоритм поиска последовательностей в Postgres демонстрирует странности: он зачем-то просматривает все значения в таблице. В моём прошлом посте использовался вот такой простой SQL-оператор для поиска значения “Captain Nemo”:
Postgres спарсил, проанализировал и спланировал запрос. Затем ExecSeqScan (встроенная функция на языке С, реализующая поиск последовательностей SEQSCAN) быстро нашла нужное значение:
Но затем по необъяснимой причине Postgres продолжил сканировать всю базу, сравнивая каждое значение с искомым, хотя оно уже было найдено!
Если бы таблица содержала миллионы значений, то поиск занял бы очень много времени. Конечно, этого можно избежать, если убрать сортировку и переписать запрос так, чтобы он останавливался на первом найденном совпадении. Но проблема более глубока, и заключается она в неэффективности самого механизма поиска в Postgres. Использование поиска последовательностей для сравнения каждого значения в таблице — процесс медленный, неэффективный и зависящий от порядка размещения записей. Должен быть другой способ!
Решение простое: нужно создать индекс.
Создание индекса
Сделать это просто, достаточно выполнить команду:
Разработчики на Ruby предпочли бы использовать миграцию add_index с помощью ActiveRecord, при которой была бы выполнена та же команда CREATE INDEX. Обычно, когда мы перезапускаем select, Postgres создаёт дерево планирования. Но в данном случае оно будет несколько отличаться:
Обратите внимание, что в нижней части используется INDEXSCAN вместо SEQSCAN. INDEXSCAN не будет сканировать всю базу в отличие от SEQSCAN. Вместо этого он использует только что созданный индекс, чтобы быстро и эффективно найти нужную запись.
Что собой представляет индекс в Postgres
Здесь отображены все параметры, которые можно использовать при создании индекса. Обратите внимание на параметр USING method: он описывает, индекс какого вида нам нужен. На той же странице приведена информация о method, аргументе ключевого слова USING:
Оказывается, в Postgres реализовано четыре разных вида индексов. Их можно использовать для различных типов данных или в зависимости от ситуации. Поскольку мы не определяли параметр USING, то index_users_on_name по умолчанию представляет собой индекс вида “btree” (B-Tree).
Что такое B-Tree и где найти о нём информацию? Для этого изучим соответствующий файл с исходным кодом Postgres:
Вот что говорится о нём в README:
Кстати, сам README является 12-страничным документом. То есть нам доступны не только полезные комментарии в коде на С, но и вся необходимая информация о теории и конкретной реализации сервера БД. Чтение и разбор кода в opensource-проектах часто является непростой задачей, но только не в Postgres. Разработчики постарались облегчить нам процесс понимания устройства их детища.
Обратите внимание, что в первом же предложении есть ссылка на научную публикацию, в которой объяснено, что такое B-Tree (а значит, и как работают индексы в Postgres): Efficient Locking for Concurrent Operations on B-Trees за авторством Лемана (Lehman) и Яо (Yao).
Что такое B-Tree
В статье описывается улучшение, внесённое авторами в алгоритм B-Tree в 1981 году. Об этом мы поговорим чуть позже. Сам алгоритм был разработан в 1972 году, так выглядит пример простого B-Tree:
Название является сокращением от англ. “balanced tree”. Алгоритм позволяет ускорить операцию поиска. Например, нам нужно найти значение 53. Начнём с корневого узла, содержащего значение 40:
Оно сравнивается с искомым значением. Поскольку 53 > 40, то далее мы следуем по правой ветви дерева. А если бы мы искали, например, значение 29, то пошли бы по левой ветви, потому что 29
B-дерево
B-дерево было впервые предложено Р. Бэйером и Е. МакКрейтом в [math]1970[/math] году.
Содержание
Структура [ править ]
Структура узла [ править ]
Структура дерева [ править ]
Назначение [ править ]
B-деревья разработаны для использования на дисках (в файловых системах) или иных энергонезависимых носителях информации с прямым доступом, а также в базах данных. B-деревья похожи на красно-чёрные деревья (например, в том, что все В-деревья с [math]n[/math] узлами имеют высоту [math]O(\log n)[/math] ), но они лучше минимизируют количество операций чтения-записи с диском.
Структуры данных во внешней памяти [ править ]
Кроме оперативной памяти, в компьютере используется внешний носитель, как правило, представляющий собой магнитные диски (или твердотельный накопитель). Хотя диски существенно дешевле оперативной памяти и имеют высокую емкость, они гораздо медленнее оперативной памяти из-за механического построения считывания.
Для того чтобы снизить время ожидания, связанное с механическим перемещением, при обращении к диску выполняется обращение одновременно сразу к нескольким элементам, хранящимся на диске. Информация разделяется на несколько страниц одинакового размера, которые хранятся последовательно друг за другом в пределах одного цилиндра (набора дорожек на дисках на одном расстоянии от центра), и каждая операция чтения или записи работает сразу с несколькими страницами. Для типичного диска размер страницы варьируется от [math]2[/math] до [math]16[/math] КБайт. После того, как головка установлена на нужную дорожку, а диск поворачивается так, что головка становится на начало интересующей нас страницы, чтение и запись становятся полностью электронными процессами, не зависящими от поворота диска, и диск может быстро читать или писать крупные объёмы данных.
В типичном приложении с B-деревом, объём хранимой информации так велик, что вся она просто не может храниться в основной памяти единовременно. Алгоритмы B-дерева копируют выбранные страницы с диска в основную память по мере надобности и записывает обратно на диск страницы, которые были изменены. Алгоритмы B-дерева хранят лишь определённое количество страниц в основной памяти в любой момент времени; таким образом, объём основной памяти не ограничивает размер B-деревьев, которые можно создавать.
Высота [ править ]
Количество обращений к диску, необходимое для выполнения большинства операций с В-деревом, пропорционально его высоте. Проанализируем высоту В-дерева в наихудшем случае.
Здесь мы видим преимущества B-деревьев над красно-черными деревьями. Хотя высота деревьев растет как [math]O(\log t)[/math] в обоих случаях (вспомним, что [math]t[/math] — константа), в случае B-деревьев основание логарифмов имеет гораздо большее значение. Таким образом, В-деревья требуют исследования примерно в [math]\log t[/math] раз меньшего количества узлов по сравнению с красно-черными деревьями в большинстве операций. Поскольку исследование узла дерева обычно требует обращения к диску, количество дисковых операций при работе с В-деревьями оказывается существенно сниженным.
Операции [ править ]
B-деревья представляют собой сбалансированные деревья, поэтому время выполнения стандартных операций в них пропорционально высоте. Однако, как уже было упомянуто выше, алгоритмы B-дерева созданы специально для работы с дисками (или другими носителями информации) и базами данных (или иными видами представления большого количества информация), минимизируя количество операций ввода-вывода.
Поиск ключа [ править ]
Если ключ содержится в текущем узле, возвращаем его. Иначе определяем интервал и переходим к соответствующему сыну. Повторяем пока ключ не найден или не дошли до листа.
Добавление ключа [ править ]
Если и родительский узел заполнен — повторяем пока не встретим незаполненный узел или не дойдем до корня. В последнем случае корень разбивается на два узла и высота дерева увеличивается. Добавление ключа в B-дереве может быть осуществлена за один нисходящий проход от корня к листу. Для этого не нужно выяснять, требуется ли разбить узел, в который должен вставляться новый ключ. При проходе от корня к листьям в поисках места для нового ключа будут разбиваться все заполненные узлы, которые будут пройдены (включая и сам лист). Таким образом, если надо разбить какой-то полный узел, гарантируется, что его родительский узел не будет заполнен.
Вставка ключа в B-дерево [math]T[/math] высоты [math]h[/math] за один нисходящий проход по дереву потребует [math]O(h)[/math] обращений к диску и [math]O(th)=O(t \log_t n)[/math] процессорного времени.
Разбиение узла [ править ]
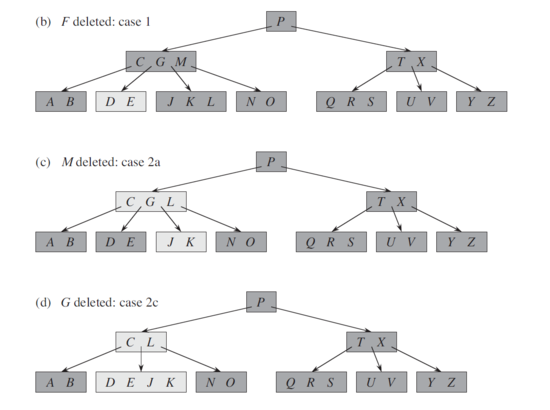
Удаление ключа [ править ]
Удаление ключа из листа [ править ]
Удаление ключа из внутреннего узла [ править ]
Перемещение ключа [ править ]
Слияние [ править ]
Ниже будет рассмотрено слияние узлов при удалении ключей, то есть слияние узлов равной степени и высоты. Для произвольных же слияний потребуется приведение сливаемых деревьев к одной степени и высоте.
Вариации B-дерева [ править ]
B+-дерево [ править ]
В B-дереве вместе с ключом может храниться только указатель на другую дисковую страницу, содержащую сопутствующую информацию для данного ключа. Существует распространённая модификация B-дерева, называемая B+-деревом, в которой, вся сопутствующая информация хранится в листьях, а во внутренних узлах хранятся только ключи и указатели на дочерние узлы. Таким образом удается получить максимально возможную степень ветвления во внутренних узлах.
B*-дерево [ править ]
Распространённая модификация B-дерева, в которой каждый внутренний узел должен быть заполнен как минимум на две трети, а не наполовину, как в случае со стандартным B-деревом. Используется в файловых системах HFS и Reiser4. В отличие от B+-деревьев, узел не разбивается на [math]2[/math] узла, если полностью заполнен. Вместо этого ищется место в уже существующем соседнем узле, и только после того, как оба узла будут заполнены, они разделяются на три узла.
2-3 дерево [ править ]
Структура данных B-дерево
Всем привет! Мы запустили новый набор на курс «Алгоритмы для разработчиков» и сегодня хотим поделиться интересным переводом, подготовленным для студентов данного курса.
В деревьях поиска, таких как двоичное дерево поиска, AVL дерево, красно-чёрное дерево и т.п. каждый узел содержит только одно значение (ключ) и максимум двое потомков. Однако есть особый тип дерева поиска, который называется B-дерево (произносится как Би-дерево). В нем узел содержит более одного значения (ключа) и более двух потомков. B-дерево было разработано в 1972 году Байером и МакКрейтом и называлось Сбалансированное по высоте дерево поиска порядка m (Height Balanced m-way Search Tree). Свое современное название B-дерево получило позже.
B-дерево можно определить следующим образом:
B-дерево – это сбалансированное дерево поиска, в котором каждый узел содержит множество ключей и имеет более двух потомков.
Здесь количество ключей в узле и количество его потомков зависит от порядка B-дерева. Каждое B-дерево имеет порядок.
B-дерево порядка m обладает следующими свойствами:
Свойство 1: Глубина всех листьев одинакова.
Свойство 2: Все узлы, кроме корня должны иметь как минимум (m/2) – 1 ключей и максимум m-1 ключей.
Свойство 3: Все узлы без листьев, кроме корня (т.е. все внутренние узлы), должны иметь минимум m/2 потомков.
Свойство 4: Если корень – это узел не содержащий листьев, он должен иметь минимум 2 потомка.
Свойство 5:Узел без листьев с n-1 ключами должен иметь n потомков.
Свойство 6: Все ключи в узле должны располагаться в порядке возрастания их значений.
Например, B-дерево 4 порядка содержит максимум 3 значения ключа и максимум 4 потомка для каждого узла.

B-дерево 4 порядка
Операции над B-деревом
Поиск по B-дереву аналогичен поиску по двоичному дереву поиска. В двоичном дереве поиска поиск начинается с корня и каждый раз принимается двустороннее решение (пойти по левому поддереву или по правому). В В-дереве поиск также начинается с корневого узла, но на каждом шаге принимается n-стороннее решение, где n – это общее количество потомков рассматриваемого узла. В В-дереве сложность поиска составляет O(log n). Поиск происходит следующим образом:
Шаг 1: Считать элемент для поиска.
Шаг 2: Сравнить искомый элемент с первым значением ключа в корневом узле дерева.
Шаг 3: Если они совпадают, вывести: «Искомый узел найден!» и завершить поиск.
Шаг 4: Если они не совпадают, проверить больше или меньше значение элемента, чем текущее значение ключа.
Шаг 5: Если искомый элемент меньше, продолжить поиск по левому поддереву.
Шаг 6: Если искомый элемент больше, сравнить элемент со следующим значением ключа в узле и повторять Шаги 3, 4, 5 и 6 пока не будет найдено совпадение или пока искомый элемент не будет сравнен с последним значением ключа в узле-листе.
Шаг 7: Если последнее значение ключа в узле-листе не совпало с искомым, вывести «Элемент не найден!» и завершить поиск.
Операция вставки в B-дерево
В В-дереве новый элемент может быть добавлен только в узел-лист. Это значит, что новая пара ключ-значение всегда добавляется только к узлу-листу. Вставка происходит следующим образом:
Шаг 1: Проверить пустое ли дерево.
Шаг 2: Если дерево пустое, создать новый узел с новым значением ключа и его принять за корневой узел.
Шаг 3: Если дерево не пустое, найти подходящий узел-лист, к которому будет добавлено новое значение, используя логику дерева двоичного поиска.
Шаг 4: Если в текущем узле-листе есть незанятая ячейка, добавить новый ключ-значение к текущему узлу-листу, следуя возрастающему порядку значений ключей внутри узла.
Шаг 5: Если текущий узел полон и не имеет свободных ячеек, разделите узел-лист, отправив среднее значение родительскому узлу. Повторяйте шаг, пока отправляемое значение не будет зафиксировано в узле.
Шаг 6: Если разделение происходит с корнем дерева, тогда среднее значение становится новым корнем дерева и высота дерева увеличивается на единицу.
Давайте создадим B-дерево порядка 3, добавляя в него числа от 1 до 10.
Insert(1):
Поскольку «1» — это первый элемент дерева – он вставляется в новый узел и этот узел становится корнем дерева.
Insert(2):
Элемент «2» добавляется к существующему узлу-листу. Сейчас у нас всего один узел, следовательно он является и корнем и листом одновременно. В этом листе имеется пустая ячейка. Тогда «2» встает в эту пустую ячейку.
Insert(3):
Элемент «3» добавляется к существующему узлу-листу. Сейчас у нас только один узел, который одновременно является и корнем и листом. У этого листа нет пустой ячейки. Поэтому мы разделяем этот узел, отправляя среднее значение (2) в родительский узел. Однако у текущего узла родительского узла нет. Поэтому среднее значение становится корневым узлом дерева.
Insert(4):
Элемент «4» больше корневого узла со значением «2», при этом корневой узел не является листом. Поэтому мы двигаемся по правому поддереву от «2». Мы приходим к узлу-листу со значением «3», у которого имеется пустая ячейка. Таким образом, мы можем вставить элемент «4» в эту пустую ячейку.
Insert(5):
Элемент «5» больше корневого узла со значением «2», при этом корневой узел не является листом. Поэтому мы двигаемся по правому поддереву от «2». Мы приходим к узлу-листу и обнаруживаем, что он уже полон и не имеет пустых ячеек. Тогда мы делим этот узел, отправляя среднее значение (4) в родительский узел (2). В родительском узле есть для него пустая ячейка, поэтому значение «4» добавляется к узлу, в котором уже есть значение «2», а новый элемент «5» добавляется в качестве нового листа.
Insert(6):
Элемент «6» больше, чем элементы корня «2» и «4», который не является листом. Мы двигаемся по правому поддереву от элемента «4». Мы достигаем листа со значением «5», у которого есть пустая ячейка, поэтому элемент «6» помещаем как раз в нее.
Insert(7):
Элемент «7» больше, чем элементы корня «2» и «4», который не является листом. Мы двигаемся по правому поддереву от элемента «4». Мы достигаем узла-листа и видим, что он полон. Мы делим этот узел, отправляя среднее значение «6» вверх к родительскому узлу с элементами «2» и «4». Однако родительский узел тоже полон, поэтому мы делим узел с элементами «2» и «4», отправляя значение «4» родительскому узлу. Только вот этого узла еще нет. В таком случае узел с элементом «4» становится новым корнем дерева.
Insert(8):
Элемент «8» больше корневого узла со значением «4», при этом корневой узел не является листом. Мы двигаемся по правому поддереву от элемента «4» и приходим к узлу со значением «6». «8» больше «6» и узел с элементом «6» не является листом, поэтому двигаемся по правому поддереву от «6». Мы достигаем узла-листа с «7», у которого есть пустая ячейка, поэтому в нее мы помещаем «8».
Insert(9):
Элемент «9» больше корневого узла со значением «4», при этом корневой узел не является листом. Мы двигаемся по правому поддереву от элемента «4» и приходим к узлу со значением «6». «9» больше «6» и узел с элементом «6» не является листом, поэтому двигаемся по правому поддереву от «6». Мы достигаем узла-листа со значениями «7» и «8». Он полон. Мы делим этот узел, отправляя среднее значение (8) родительскому узлу. Родительский узел «6» имеет пустую ячейку, поэтому мы помещаем «8» в нее. При этом новый элемент «9» добавляется в узел-лист.
Insert(10):
Элемент «10» больше корневого узла со значением «4», при этом корневой узел не является листом. Мы двигаемся по правому поддереву от элемента «4» и приходим к узлу со значениями «6» и «8». «10» больше «6» и «8» и узел с этими элементами не является листом, поэтому двигаемся по правому поддереву от «8». Мы достигаем узла-листа со значением «9». У него есть пустая ячейка, поэтому туда мы помещаем «10».
Предлагаем вам самостоятельно на практике понять, как устроены В-деревья, воспользовавшись этой визуализацией.
Ждем всех на бесплатном открытом уроке, который пройдет уже 12 июля. До встречи!