инженерная графика и начертательная геометрия в чем разница

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ КАК ФАКТОР УСПЕШНОЙ ПОДГОТОВКИ БУДУЩЕГО ИНЖЕНЕРА

Для успешного решения этой задачи необходимо уже в школе учить школьников видеть в окружающих предметах образующие их форму геометрические тела, учить узнавать геометрические формы в тех предметах, которые им попадаются на глаза чуть ли не ежедневно. Эта способность видеть геометрию вокруг себя есть ценнейшее свойство, которое приводит к образованию абстрактных понятий геометрических фигур, таких как прямоугольник, окружность, призма, цилиндр и т.д.

Основная цель изучения научить воспринимать форму предмета, а также развивать пространственное мышление, развивать творческие способности, формировать геометрические представления [2].

Выпускник школы должен быть готов к восприятию начертательной геометрии, но все равно считаю, что на стартовом этапе обучения начертательной геометрии необходимо проводить следующие работы по: обобщению и «выравниванию» знаний о геометрических телах и фигурах; обучению анализу геометрической формы объекта как основы понимания его конструкции и умения читать чертежи.

Студент первокурсник, приступающий к систематическому изучению начертательной геометрии, нуждается в развитии его пространственных представлений, пространственного воображения, и особенно, пространственного мышления. Термин пространственное воображение, обозначает человеческую способность четко представлять трехмерные объекты в деталях и цветовом исполнении [3].

Всем известно, что начертательная геометрия развивает у студентов пространственное мышление, чёткую логику и создание необходимой теоретической базы для дальнейшей учёбы. Дальнейшая учеба подразумевает под собой изучение более сложной дисциплины, такой как, инженерная графика. Но, как известно из психологии восприятия, подобным видом мышления обладают всего несколько процентов студентов. У остальных оно полностью отсутствует. И поэтому студенты считают этот предмет «трудным». Зачастую, не то чтобы студенту было непонятно: «Зачем это нужно?», преподаватель задаётся вопросом: «Как?». В итоге, попытка развить пространственное мышление у всех студентов, ни к чему не приводит.

До недавнего времени начертательная геометрия применялась в решении сложных инженерно-технических задач, используя точные графические методы. Заключённая в строгие рамки математическая дисциплина, может решать сложные задачи, обходясь без пространственного представления об объекте.

Классическая математика рассматривает эту дисциплину, как моделирование трёхмерного пространства для разного рода задач, используя графический метод. Базируется начертательная геометрия на собственном методе – проецировании. В этом случае все схемы и чертежи нужно рассматривать как двухмерные эквиваленты пространственных объектов.

Как уже давно известно, что при переходе от изучения начертательной геометрии к изучению дисциплины «Инженерная графика», даже у «слабых» студентов появляются новые силы к её изучению и пониманию. Это в большей степени объясняется тем, что происходит переход от двухмерных графических изображений к трёхмерным чертежам. В этом случае абстрактное мышление очень часто заменяется практическим, более лёгким для понимания многих учащихся. Но, опять же, учащиеся, хорошо понимающие все чертежи, связанные с техническими объектами, оказываются совершенно беспомощными при начертании схем абстрактных моделей.

Исходя из этого можно уверенно сказать, что начертательная геометрия не может быть основой для изучения инженерной графики, более сложной для понимания дисциплины. Хотя, без некоторых её аспектов трудно понять всю структуру более сложного трёхмерного пространства, которое изучает инженерная графика. Кроме того, начертательная геометрия является предметом, на котором основывается дальнейшее образование будущего инженера.

Обучение инженерной графике в настоящее время начинается с изучения правил отображения объектов на плоскости по методу Монжа, начиная с простых геометрических объектов (плоскостей, призм, пирамид, цилиндров и т.д.). Затем рассматривается создание чертежей объектов, похожих на реальные детали и сборочных единиц и попутно изучаются основные типы конструкторской документации, соответствующие разным стадиям проектирования.

Метод Монжа – ортогональное проецирование элементов трехмерного пространства на две взаимно-перпендикулярные плоскости, в результате которого получается двухкартинный плоский чертеж, обладающий метрической определенностью и обратимостью.

Любой инженер должен уметь пользоваться вычислительной техникой, которая в состоянии смоделировать производственные процессы и работу технических объектов, включая эти объекты. Но, это невозможно без обращения к объектам расширенного Евклидового пространства, их свойств, правил преобразования и без соответствующего образования самого пользователя.

Основные задачи этой дисциплины (начертательная геометрия) будут:

-образование формальной модели Евклидова пространства

— систематизация подхода к решению позиционных задач

— выработка умения моделировать сложные трёхмерные объекты, системы и технические формы, сложные, в основном

Вот поэтому-то, решение подобных задач ставится во главе учебного процесса. Необходимо повысить время изучения таких программ, как построение кривых и конструирование поверхностей. Использование в профессиональной деятельности метода 3D проектирования [1,4], требует полного понимания между ортогональными чертежами с метрически определёнными «наглядными изображениями».

У современного студента необходимо повысить навыки конструирования геометрических форм по заданным свойствам. Необходимо усвоить, что нельзя решать задачу одним и тем же способом, если в одном случае объект находится на чертеже, а другом в пространстве. Потому что чертёж служит только для визуализации одного единственного вида у объекта, а находясь в пространстве, мы в состоянии разглядеть конечный результат.

В конце хочу добавить, что полное понимание, конечно же, приходит только после практических занятий на производстве или применении этих знаний непосредственно на практике. Можно только пожелать удачи студентам при изучении сложных графических задач в начертательной геометрии и инженерной графике.

1. Борисенко И. Г. Инновационные технологии в преподавании начертательной геометрии при формировании профессиональных компетенций. / И.Г. Борисенко// Вестник Иркутского ГТУ. – 2011. –№ 12, с. 355-357.

2. Джуган Т.В., Федотова Н.В. Пространственное мышление школьника и студента как фактор развития творческой личности // Современные наукоемкие технологии. –2008. – № 9 – С. 24-27

3. Русинова Л. П. Развитие пространственного мышления у студентов в начале изучения курса «Начертательная геометрия» [Текст] / Л. П. Русинова // Молодой ученый.— 2012. — №3. — С. 391-394.

4. Савельева Н.Н. Применение информационных технологий при организации процесса подготовки студентов для высокотехнологичных предприятий / Н.Н. Савельева // Информационные ресурсы в образовании: материалы Международной научно-практической конференции. – Нижневартовск, 2013. – С. 68-71

Источник

Поступив в технический или строительный ВУЗ многие однокурсники сталкиваются со сложными предметами. Для некоторых студентов сложнее всего разобраться в начертательной геометрии и понять инженерную графику. Преимущественно практические все студенты в самом начале начинают изучение именно с начертательной графики, так уж устроены образовательные программы российских технических высших учебных заведений. Обосновывается это необходимостью развить у обучающихся необходимых навыков пространственного мышления. Развить навыки пространственного мышления можно пройдя обучающие курсы 101 Курс по Автокаду. Также при изучении начертательной геометрии в сознании студента появятся теоретические основы для того, чтобы в дальнейшем изучать инженерную графику. Но большое число психологов считают, что пространственное мышление дано не всем людям, и задатки к нему есть у ограниченного числа студентов.

Преподаватели подчеркивают, что переходя от изучения начертательной геометрии к изучению инженерной графики, многие студенты значительно повышают уровень своей успеваемости. Это связано с тем, что инженерная графика предмет имеющий практическую направленность в отличии от начертательной геометрии, которая требует значительного уровня абстрактного мышления от студентов. Поэтому работу с чертежами при изучении инженерной графики студенты выполняют более успешно, чем в начертательной геометрии.

Начертательная геометрия в свою очередь должна решать задачи формирования формальной модели расширенного Евклидового пространства у обучающихся, системного подхода к решению позиционных и метрических задач, умения моделировать сложные технические формы, системы и процессы.

Чтобы решить эти задачи, необходимо пересмотреть современную учебную программу в наших вузах. Так как сейчас для выполнения этих задач не хватает количества часов для изучения некоторых разделов начертательной геометрии и инженерной графики, а также следует обратить большое внимание на формирование у студентов необходимых навыков проектирования различных геометрических форм и объектов.

Источник

Инженерная графика

Инженерная графика – это учебная дисциплина, в которой изучаются теория, методы и правила выполнения чертежей.

Теорией инженерной графики является начертательная геометрия, представляющая собой одну из ветвей обширной области геометрии и отличающаяся от других своими методами решения. В начертательной геометрии пространственные отношения и формы тел познаются с помощью их изображения. Поэтому наиболее существенными требованиями к чертежам являются следующие:

1) чертеж должен быть наглядным (вызывать пространственное представление изображаемого предмета);

2) чертеж должен быть обратимым (чтобы по нему можно было точно воспроизвести форму и размеры изображаемого предмета);

3) чертеж должен быть достаточно простым с точки зрения его графического выполнения;

4) графические операции, выполняемые на чертеже, должны давать достаточно точные решения.

ТРЕБОВАНИЯ К УРОВНЮ ЗНАНИЙ И УМЕНИЙ СТУДЕНТОВ, ПРИСТУПАЮЩИХ К ИЗУЧЕНИЮ ДИСЦИПЛИН «НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ» И «ИНЖЕНЕРНАЯ ГРАФИКА»

Студент должен знать:

-основные понятия стереометрии (множество, точка, прямая, плоскость, расстояния);

-свойства параллельной проекции;

-ортогональное (прямоугольное) проецирование;

-взаимное расположение прямых и плоскостей (параллельность и перпендикулярность);

-многогранники, их развертки;

-правила построения чертежей предметов в системе прямоугольных проекций.

Студент должен уметь:

-мысленно выделять из предметов, представляющих собой сочетание различных геометрических фигур, составные элементы;

-воссоединять элементы в целостный предмет;

-выявлять отношения сходства и различия между соотносимыми фигурами;

-строить третью проекцию детали по двум данным;

-определять недостающие проекции заданных точек, принадлежащих поверхностям данных деталей.

ОРГАНИЗАЦИЯ РАБОТЫ СТУДЕНТОВ

Продолжительность обучения данным дисциплинам составляет три семестра для специальностей механического профиля, два семестра для всех остальных. В работу студентов включается:

1) изучение начертательной геометрии как теоретической основы построения чертежей геометрических тел;

2) решение на чертежах задач методами начертательной геометрии;

3) изучение государственных стандартов по выполнению и оформлению чертежей;

4) изучение технического черчения (чертежи изделий);

5) выполнение индивидуальных графических заданий, предназначенных для закрепления знаний по методам и правилам формирования изображений и развития умений и навыков их графического построения.

Каждый студент в процессе обучения выполняет индивидуальные задания по определенным темам данных дисциплин. На каждое задание в зависимости от его сложности отводится от 3 до 5 недель. Сроки выполнения заданий включаются в общий график учебного процесса студентов данной специальности и контролируются кафедрой и деканатом. В течение каждого семестра студенты выполняют три домашних контрольно-графических задания. Оценка задания включает в себя знание теории и качество его графического выполнения.

ФОРМЫ РАБОТЫ И ОТЧЕТНОСТИ СТУДЕНТОВ

Предусмотрены следующие формы работы:

1) аудиторные занятия – лекции и практика в соответствии с утвержденным расписанием;

3) консультации после аудиторных занятий по расписанию кафедры.

Лекции проводятся по потокам, практические занятия – по группам. При этом каждая группа делится на две подгруппы, в каждой из которых занятия проводит один преподаватель. Самостоятельная работа студентов представляет собой изучение лекционного материала; решение задач в соответствии со способами и алгоритмами, рассмотренными на лекциях и практических занятиях; изучение государственных стандартов, правил выполнения и оформления чертежей по требованиям технической и конструкторской документации, соответствующим ЕСКД; выполнение карандашом индивидуальных графических заданий на чертежной бумаге стандартных форматов (ГОСТ 2.301 – 68). Консультации и прием графических заданий осуществляются, как и практические занятия, по подгруппам. Итоги работы студентов подводятся в течение семестра, а также в конце семестра на зачете или экзамене в зависимости от объема программы данной специальности. Работа студентов оценивается по пятибалльной шкале или по рейтинговой системе.

СОДЕРЖАНИЕ ВОПРОСОВ ПО ДИСЦИПЛИНАМ

Изучение начертательной геометрии включает в себя следующие вопросы:

— метод проекций; центральное, параллельное, прямоугольное проецирование и их свойства;

— образование чертежа на двух и трех плоскостях проекций;

— аксонометрические проекции (образование, виды, показатели искажения, прямоугольные изометрическая и диметрическая проекции, изображение окружности);

— способы преобразования чертежа;

— проекции точки на две и три плоскости проекций, прямоугольные координаты точки;

— задание и изображение на чертеже прямой линии, положение относительно плоскостей проекций, две прямые, изображение пересекающихся, параллельных и скрещивающихся прямых, конкурирующие точки;

— задание и изображение на чертеже окружности и винтовой линии;

— задание и изображение на чертеже плоскости, положение относительно плоскостей проекций;

— определение и образование поверхностей, задание и изображение на чертеже, определитель, каркас и очерк поверхности, поверхности вращения, торсовые, винтовые;

— позиционные задачи, алгоритмы их решения;

— принадлежность точки и линии плоскости, поверхности;

— параллельность прямой и плоскости, двух плоскостей;

— перпендикулярность прямой и плоскости, двух плоскостей;

— пересечение прямой с плоскостью;

— взаимное пересечение плоскостей;

— сечение поверхностей вращения плоскостями частного положения;

— пересечение соосных поверхностей вращения;

— пересечение поверхностей (применение секущих сфер и секущих плоскостей частного положения);

— метрические задачи (определение расстояний от точки до прямой и плоскости, определение углов, построение разверток многогранников, цилиндрических, конических поверхностей вращения).

В начертательной геометрии можно выделить три типа задач: построение проекций геометрических объектов, позиционные и метрические задачи.

Для построения изображений геометрических объектов используется метод проецирования на плоскость.

Позиционными называются задачи установления взаимного положения и принадлежности геометрических элементов.

Метрические – это задачи определения по чертежу натуральных величин отрезков (расстояний), истинных углов и других размеров.

Логика решения задач в начертательной геометрии выражается в виде алгоритмов, отражающих определенную последовательность выполнения графических операций. Эти алгоритмы могут иметь форму словесного описания последовательности графических действий или быть в виде формализованной записи с использованием символов.

Изучение технического черчения включает в себя:

— изображения предметов (виды, разрезы, сечения, построение по двум данным изображениям третьего);

— изображение резьбовых изделий и их соединений;

— изображение шпоночных и шлицевых соединений;

— изображение соединений сваркой, пайкой и склеиванием;

— выполнение эскизов деталей с натуры;

— выполнение чертежей сборочных единиц и эскизов их деталей;

— выполнение чертежей деталей по заданным чертежам сборочных единиц;

— выполнение чертежей по специальности обучения студентов.

Широкое разнообразие чертежей требует единых правил и условностей их изготовления. Они регламентируются государственными стандартами. Все стандарты объединены под общим названием «Единая система конструкторской документации» (ЕСКД). Все стандарты, предусмотренные ЕСКД, распределяются по следующим классификационным группам:

0 – общие положения;

1 – основные положения;

2 – классификация и обозначение изделий в конструкторских документах;

3 – общие правила выполнения чертежей;

4 – правила выполнения чертежей в машиностроении и приборостроении;

ние, внесение изменений);

6 – правила выполнения эксплуатационной и ремонтной документации;

7 – правила выполнения схем;

8 – правила выполнения строительных документов судостроения;

9 – прочие стандарты.

В ЕСКД все стандарты имеют определенную структуру обозначений и названий. Например, ГОСТ 2.303 – 68 «Линии» обозначает, что стандарт входит в комплекс ЕСКД, которому присвоен номер 2, номер стандарта – – шифр классификационной группы, 03 – порядковый номер стандарта в группе), год регистрации 1968, «Линии» – название.

В инженерной графике изучаются ГОСТы, входящие в группы 1, 2, 3, 4 и 7.

Источник

Виды, разрезы, сечения в начертательной геометрии с примерами

Содержание:

Виды, разрезы, сечения:

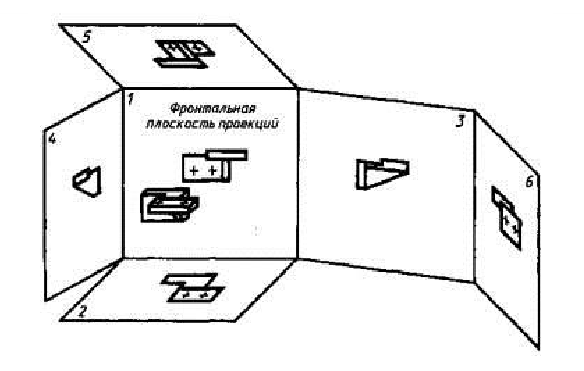
Изображения предметов на чертеже следует выполнять по методу прямоугольного проецирования. При этом предмет предполагается расположенным между наблюдателем и соответствующей плоскостью проекций (см. рисунок 11.1) [4].

Рисунок 11.1- Изображение предмета на шести гранях куба

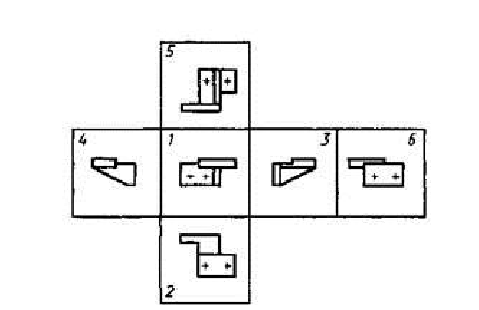
За основные плоскости проекций принимают шесть граней куба; грани совмещают с плоскостью, как показано на рисунке 11.2. Грань 6 допускается располагать рядом с гранью 4.

Изображение на фронтальной плоскости проекций принимается на чертеже в качестве главного. Предмет располагают относительно фронтальной плоскости проекций так, чтобы изображение на ней давало наиболее полное представление о форме и размерах предмета.

Масштаб изображений, расположенных в непосредственной проекционной связи друг с другом на основных плоскостях проекций, принимают за масштаб выполнения документа и записывают в соответствующем реквизите основной надписи (ГОСТ 2.104).

Для уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности предмета с помощью штриховых линий.

Количество изображений (видов, разрезов, сечений) должно быть наименьшим, но обеспечивающим полное представление о предмете при применении установленных в соответствующих стандартах условных обозначений, знаков и надписей.

В зависимости от содержания изображения разделяют на виды, разрезы, сечения.

Виды

Вид предмета (вид): Ортогональная проекция обращенной к наблюдателю видимой части поверхности предмета, расположенного между ним и плоскостью проецирования [4].

Главный вид предмета (главный вид): Основной вид предмета на фронтальной плоскости проекции, который дает наиболее полное представление о форме и размерах предмета, относительно которого располагают остальные основные виды.

Дополнительный вид предмета (дополнительный вид): Изображение предмета на плоскости, непараллельной ни одной из основных плоскостей проекций, применяемое для неискаженного изображения поверхности, если ее нельзя получить на основном виде.

Местный вид предмета (местный вид): Изображение отдельного ограниченного участка поверхности предмета.

Основной вид предмета (основной вид): Вид предмета, который получен путем совмещения предмета и его изображения на одной из граней пустотелого куба, внутри которого мысленно помещен предмет, с плоскостью чертежа. Основной вид предмета может относиться к предмету в целом, его разрезу или сечению.

Установлены следующие названия видов, получаемых на основных плоскостях проекций (основные виды, рисунок 11.2):

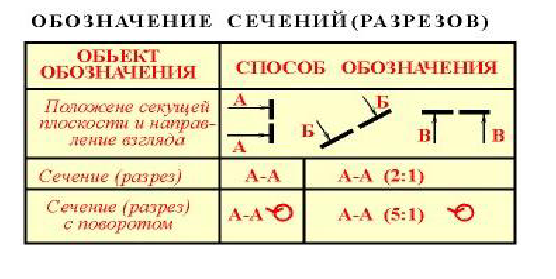
Если виды сверху, слева, справа, снизу, сзади не находятся в непосредственной проекционной связи с главным изображением (видом или разрезом, изображенным на фронтальной плоскости проекции), то направление проецирования должно быть указано стрелкой около соответствующего изображения. Над стрелкой и над полученным изображением (видом) следует нанести одну и ту же прописную букву.

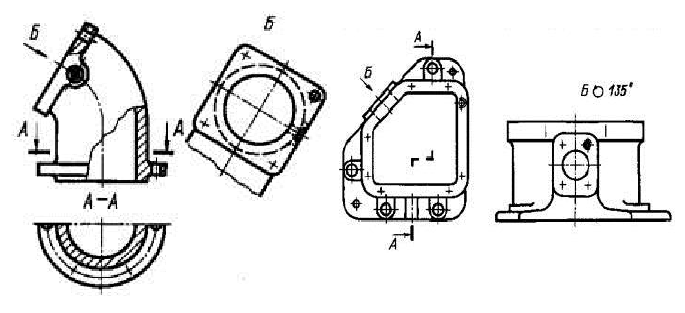
Если какую-либо часть предмета на чертеже невозможно показать без искажения формы и размеров, то применяют дополнительные виды, получаемые на плоскостях, непараллельных основным плоскостям проекций (см. рисунки 11.3).

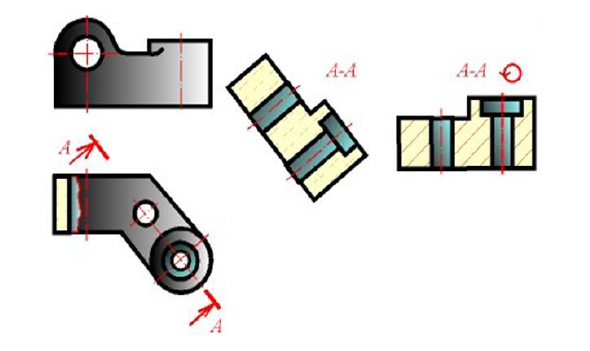
Дополнительный вид должен быть отмечен на чертеже прописной буквой (см. рисунки 11.3), а у связанного с дополнительным видом изображения предмета должна быть поставлена стрелка, указывающая направление взгляда, с соответствующим буквенным обозначением (например, стрелка Б, рисунки 11.3).

Дополнительный вид допускается повертывать, но с сохранением, как правило, положения, принятого для данного предмета на главном изображении, при этом обозначение вида должно быть дополнено условным графическим обозначением 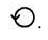При необходимости указывают угол поворота (см. рисунок 11.3).

Местный вид может быть ограничен линией обрыва, по возможности в наименьшем размере, или неограничен. Местный вид должен быть отмечен на чертеже подобно дополнительному виду.

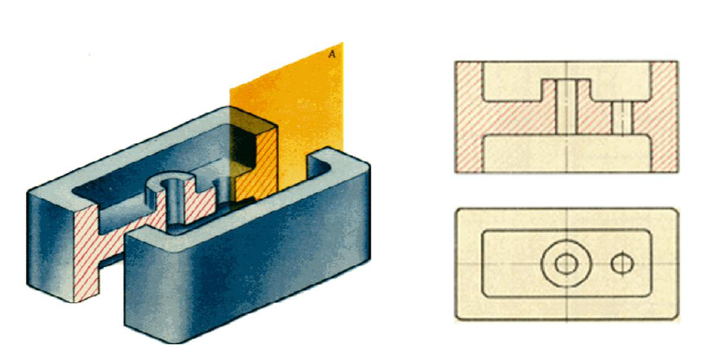
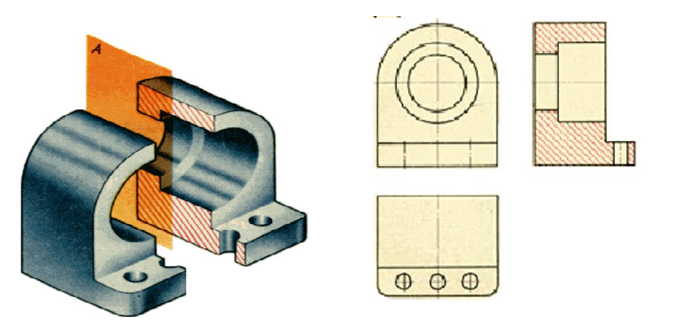
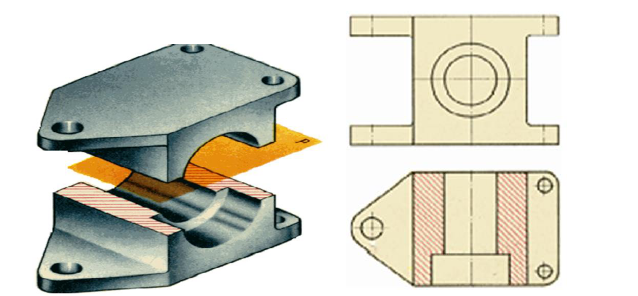
Разрезы

Выявление фоpмы внутpенних повеpхностей пpедмета пpи помощи штpиховых линий значительно затpудняет чтение чеpтежа, сoздает пpедпосылки для непpавильного его толкования, усложняет нанесение pазмеpов и условных обозначений. Поэтому для выявления внутpенней (невидимой) конфигуpации пpедмета пpименяют условные изобpажения – pазpезы и сечения.

Принцип выполнения разрезов заключается в том, что условно представляют отсеченной и отнятой одну из частей детали так, что становится ясно внутреннее очертание оставшейся части детали.

При этом линии невидимого контура станут видимыми и будут изображаться сплошными основными линиями.

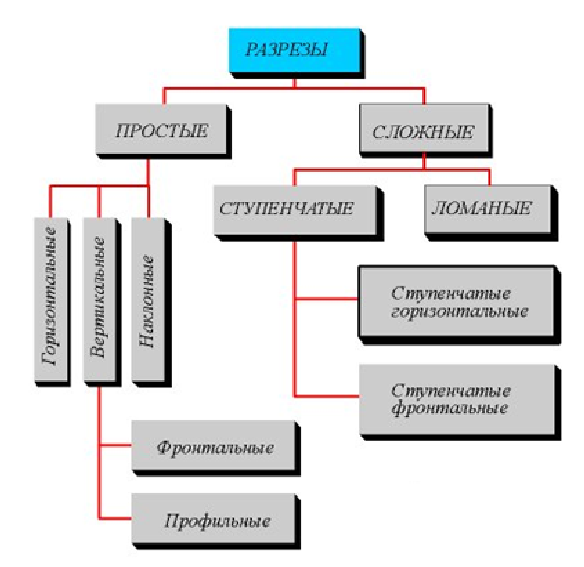
Классификация разрезов

В зависимости от числа секущих плоскостей разрезы бывают

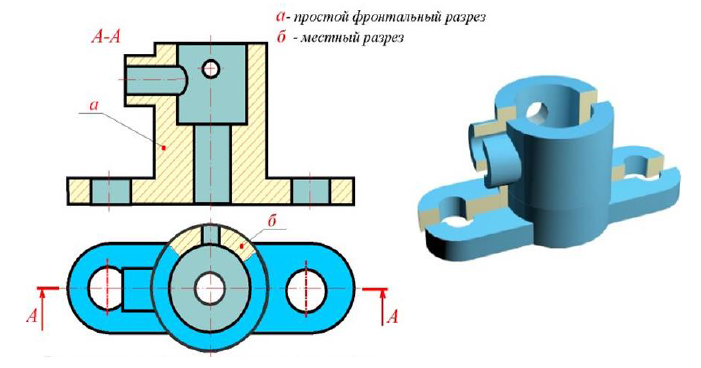
Простые разрезы

В зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций простые разрезы делятся на:

Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций, профильным, если секущая плоскость параллельна профильной плоскости проекций.

Положение секущей плоскости не отмечают и pазpез надписью не сопpовождают, если одновpеменно выполняются тpи условия:

Веpтикальный pазpез

Веpтикальный pазpез, когда секущая плос-кость не паpаллельна фpонтальной или пpофильной плоскостям пpоекций.

Веpтикальный наклонный pазpез допускается выполнять с повоpотом до положения, соответствующего пpинятому для данного пpедмета на главном изобpажении. В этом случае к обозначению должен быть добавлен знак «повернуто»

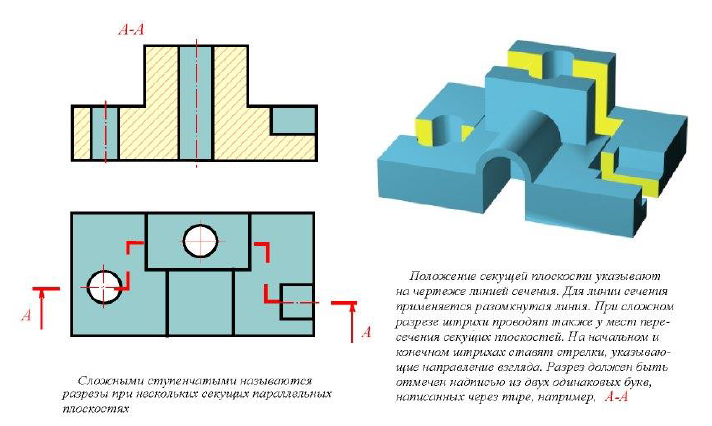
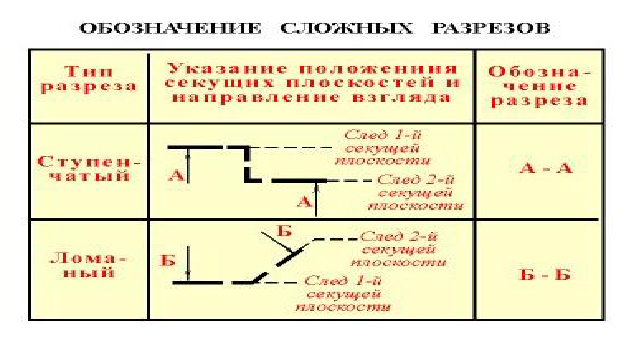
Сложные разрезы

Сложный ступенчатый разрез

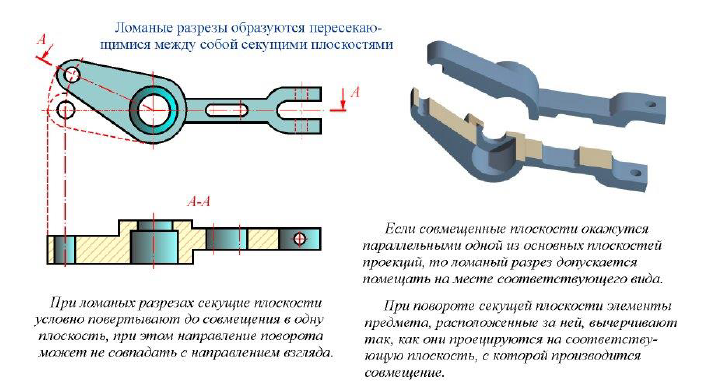
Сложный ломаный разрез

Рисунок 11.11- Сложный ломаный разрез рычага

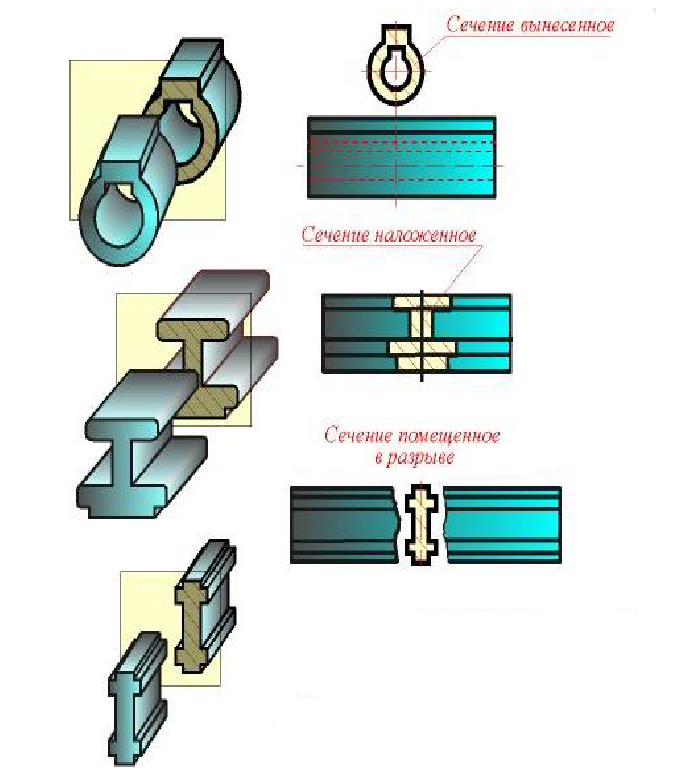
Сечения

Сечением называется изобpажение фигуpы, получающейся пpи мысленном pассечении пpедмета одной или несколькими плоскостям.

Hа сечении показывают только то, что получается непосpедственно в секущей плоскости.

Рисунок 11.12 – Сечение вынесенное, наложенное, в разрыве

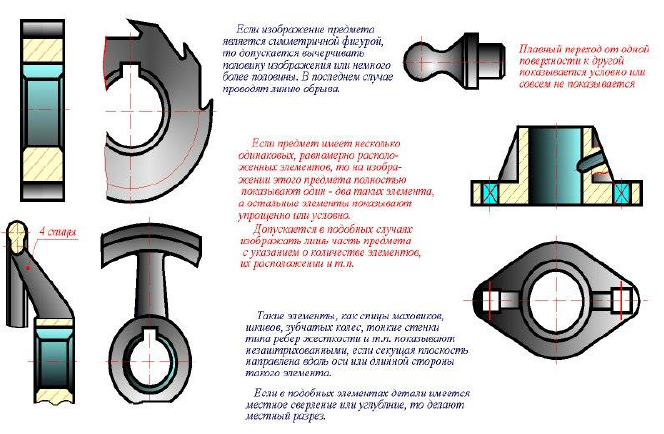
Условности и упрощения

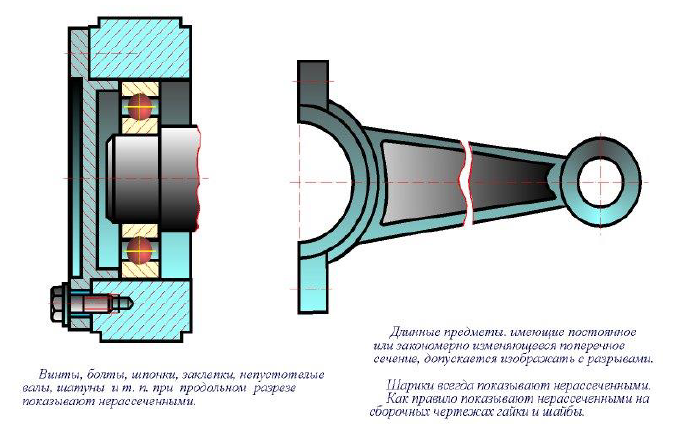
Рисунок 11.12 – Условности и упрощения на деталях

Рисунок 11.13 – Условности и упрощения на сборочных чертежах и деталях

Если изобpажение пpедмета является симметpичной фигуpой, то допускается вычеpчивать половину изобpажения или немного более половины.

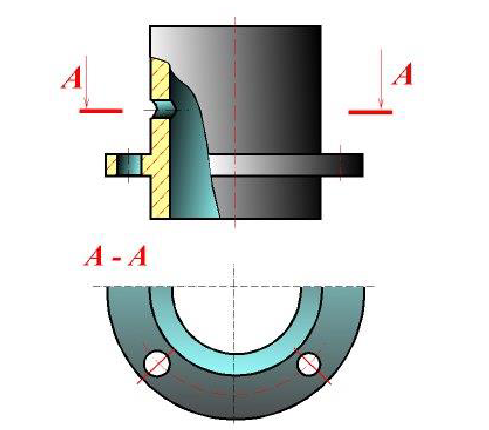
Допускается изобpажать в pазpезе отвеpстия, pасположенные на кpуглом фланце, когда они не попадают в секущую плоскость.

Рисунок 11.14 – Условности для симметpичных деталей

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник