Сэмплирование что это такое
Семплирование: когда возникает и как от него избавиться?
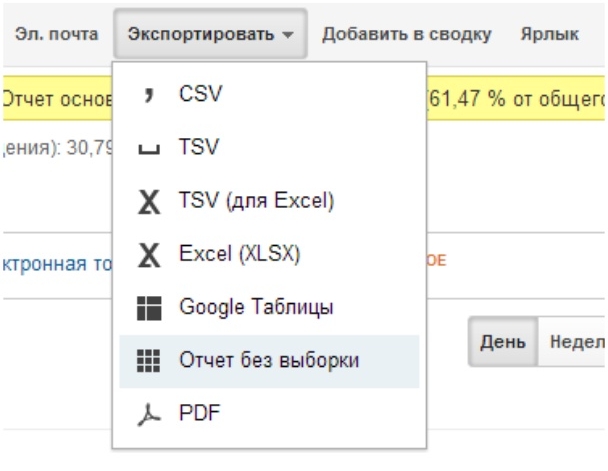
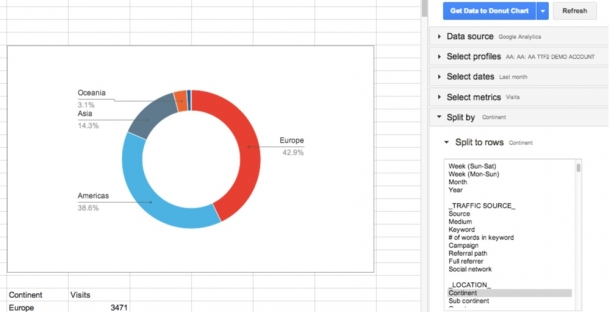
Создать отчёт в Google Analytics. Простая задача, пока не увидишь такое уведомление:
Что это значит? Google Analytics берёт 10% данных. Домножает их на 10. И говорит, что 100% так бы себя и вели.
Это классно, когда работаешь с большими цифрами. Отчёт готовится быстро.
Но есть и недостатки. Представьте, что вы получили 1 из 10 кусочков торта. И нужно понять, сколько на торте свечек. Если вам попался кусок без свечки — вы скажете, что 0. Если с 1 свечкой — то 10. А если 2 — то 20.
Так же и в аналитике. Вы выгружаете статистику по ключевым словам. Analytics построил отчёт на 10% данных. В эти данные вошёл запрос, который ввёл только 1 человек. Но в семплированном отчёте вы увидите, словно этот запрос привел 10 людей.
Семплирование искажает данные. Как от него избавиться?
Решение 1. Google Analytics Premium
Проблема в том, что в GA Premium тоже есть семплирование. Но можно выгрузить выборку на сторонний ресурс. Например, в Excel. И там уже обрабатывать сырые данные.
Плати, не плати. Excel все равно понадобится.
Решение 2. Попытаться обойти семплирование
Чтобы обойти семплирование, нужно понимать, как оно возникает.
Когда возникает семплирование?
1. Нестандартный отчёт
2. Много данных
Чем больше информации нужно выгрузить — тем чаще встречается семплирование.
Как обойти семплирование?
1. Короткие периоды времени
Например, вы создаёте отчёт за год. Возникает семплирование. Вместо 1-го большого создайте 12 маленьких отчетов. На каждый месяц. Выгрузка данных займёт больше времени. Зато семплирование может отключиться.
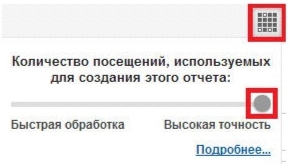
2. Высокая точность вместо быстрой обработки
При создании отчётов в Google Analytics кликните по такой иконке:
И порог семплирования умножается в 2 раза. Отчёт строился на 10% данных? После выбора «Высокой точности» он будет дольше грузиться, но захватит уже 20% выборки.
3. Отфильтрованные заранее представления (Views)
Что такое отфильтрованные представления? Например, это представления с посещениями только из контекстной рекламы. Или с посещениями только по какой-то конкретной кампании.
Если вы планируете создать отчет и сегментировать в нём данные, поменяйте порядок действий. Создайте заранее отсегментированные представления. И выгружайте отчёты отдельно для каждой части данных.
Но это не всегда работает. Сложные отчёты даже в фильтрованном представлении могут быть семплированными.
4. Упрощённый запрос
Сделайте выборку проще, чтобы меньше нагружать Analytics. Например, вы привыкли фильтровать какой-то параметр по регулярному выражению. Попробуйте профильтровать по точному. Возможно, часть данных будет уже проще обработать в Excel.
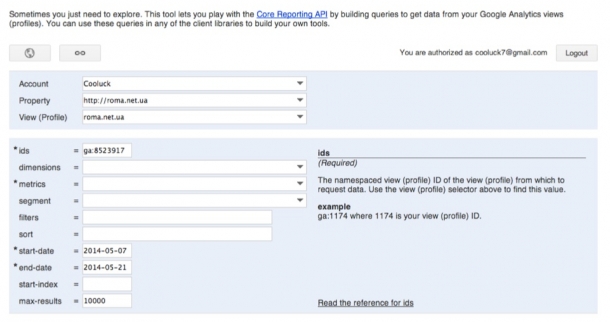
5. Решения на основе API — Google Analytics Query Explorer 2
Google Analytics Query Explorer 2
Это песочница от Google. Она использует тот же язык запросов. Здесь вы можете строить запросы. Делиться ссылкой с коллегой.
Преимущества
Ограничения
Как работает? Строите запрос — какие данные хотите получить. Даёте ссылку на отчёт программисту. Просите выгрузить данные по API.
Обратите внимание! Google Analytics Query Explorer выгружает до 10 тыс. строк за один раз.
Существуют другие инструменты, с помощью которых можно выгружать данные с Google Analytics. Они защищают от семплирования. А для особо крупных проектов — значительно уменьшают его. Читайте о том, какие бывают источники данных для интернет-проекта, кроме Google Analytics.
Supermetrics Data Grabber
Это дополнение к Excel. Работает с Windows Excel 2003+ и с Mac Excel 2011.
Вытягивает данные из Google Analytics, Google AdWords, Bing Ads, Facebook, Youtube, Twitter.
Стоимость: 39-174$ в месяц.
Как работает? Выбираете период, метрики и ставите галочку «Попытаться избавиться от семплирования». И выгружаете отчёт.
Supermetrics for Google Docs
Дополнение к Google Docs, Google Sheets.
Вытягивает данные из Google Analytics, Google AdWords, Google Webmasters Tools, Bing Ads, Facebook, Youtube, Twitter, Database.
Стоимость: бесплатно, 49-99$ в месяц.
Платная версия частично решает проблему семплирования. Бесплатная — нет.
Как работает? В Google Docs появляется колонка справа. В ней можно выбрать, по каким параметрам строить отчет. Выгружает до 100 000 строк.
Analytics Canvas
Программа, которая работает на Windows XP, Vista, 7, 8
Вытягивает данные из Google Analytics, Bing Ads, файлы Excel, Database (SQL etc.)
Стоимость — 49-798$ в месяц
Преимущества. Экспортирует затраты в Google Analytics.
Как работает? Как база данных. Выгружает информацию из Google Analytics. Может объединять разные куски данных между собою. Например, из CRM выгрузили номер заказа и сумму. А из Google Analytics — номер заказа и рекламный источник. Инструмент объединят данные в единую таблицу.
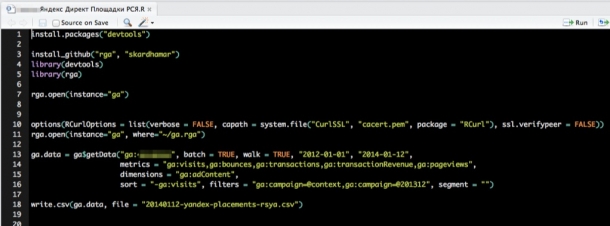
Язык программирования «R» + дополнение RGA
Работает с Windows, Mac.
Вытягивает данные из Google Analytics.
Преимущества. Бесплатный инструмент.
Как работает? Специальный скрипт подгружает несколько библиотек. Идёт к API на Google Analytics.
Чтобы обойти семплирование, обратите внимание на 2 параметры: batch и walk.
Batch. Делит выборку на группы по 10 000 строк. Выгружает данные порциями. Как Google Analytics Query Explorer.Потом склеит все в один файл.
Walk. Полезен, когда выгружаете данные за большой период. Параметр делит данные по дням. Если вы создаёте отчёт за 1 год, параметр walk поделит его на 365 отдельных блоков. Выгрузка данных займет больше времени, зато вы избавитесь от семплирования.
Файлы для установки, инструкцию по настройке и скрипт для R+RGA смотрите на Roman.ua.
Не довольствуйтесь малым. Анализируйте все данные!
Вероятностные модели: сэмплирование
И снова здравствуйте! Сегодня я продолжаю серию статей в блоге Surfingbird, посвящённую разным методам рекомендаций, а также иногда и просто разного рода вероятностным моделям. Давным-давно, кажется, в прошлую пятницу летом прошлого года, я написал небольшой цикл о графических вероятностных моделях: первая часть вводила основы графических вероятностных моделей, во второй части было несколько примеров, часть 3 рассказывала об алгоритме передачи сообщений, а в четвёртой части мы кратко поговорили о вариационных приближениях. Цикл заканчивался обещанием поговорить о сэмплировании — ну что ж, не прошло и года. Вообще говоря, в этом мини-цикле я поведу речь более предметно о модели LDA и о том, как она помогает нам делать рекомендации текстового контента. Но сегодня начну с того, что выполню давнее обещание и расскажу о сэмплировании в вероятностных моделях — одном из основных методов приближённого вывода. 
В чём задача
Прежде всего я напомню, о чём мы вообще говорим. Один из основных инструментов машинного обучения — это теорема Байеса:
Здесь D — это данные, θ — параметры модели, которые мы хотим обучить, а — это распределение θ при условии имеющихся данных D; про теорему Байеса мы уже подробно говорили одной из предыдущих статей. В машинном обучении мы, как правило, хотим найти апостериорное распределение , а затем предсказать новые значения переменных . В сложных графических моделях всё это, как мы обсуждали в предыдущих сериях, обычно сводится к тому, что у нас есть большое и запутанное распределение разнообразных случайных величин , которое раскладывается в произведение распределений попроще, и наша задача — провести маргинализацию, т.е. суммировать по части переменных или найти ожидание функции от части переменных. Заметим, что все наши задачи так или иначе сводятся к тому, чтобы подсчитать математическое ожидание разных функций при условии сложного распределения, обычно условного распределения модели, в которую подставлены значения некоторых переменных. Также можно считать, что мы умеем считать значение совместного распределения в любой его точке — это обычно несложно следует из общего вида модели, а сложность как раз в том, чтобы по куче этих переменных просуммировать-проинтегрировать.
Мы уже знаем, что точный вывод вести сложно, и эффективные алгоритмы получаются только для случая фактор-графа без циклов или с маленькими циклами. Однако реальные модели часто содержат кучу переменных, которые связаны друг с другом достаточно плотно и образуют массу циклов. Мы немного говорили о вариационных приближениях — одном возможном способе преодолеть возникающие трудности. А сегодня я расскажу о другом, ещё более популярном методе — о сэмплировании.
Приближение Монте-Карло
Идея проста до чрезвычайности. Мы уже выяснили, что в принципе всё, что нам нужно, выражается в виде ожиданий разнообразных функций по нашему сложному и запутанному распределению p(x). Как подсчитать ожидание функции по распределению? Если мы умеем сэмплировать из этого распределения, т.е. брать случайные точки по распределению p(x), то ожидание любой функции можно приблизить как среднее арифметическое в сэмплированных точках:
Например, чтобы посчитать среднее (матожидание), нужно усреднить по сэмплам x.
Таким образом, вся наша задача фактически сводится к тому, чтобы научиться сэмплировать точки по распределению при условии, что мы можем в любой точке считать значение этого распределения.
В чём тут сложность
Что же делать: сэмплируем под графиком
Несмотря на все вышеперечисленные сложности, сэмплирование делать всё-таки возможно, и это действительно один из главных приёмов приближённого вывода. Более того, как мы скоро увидим, делать сэмплирование совсем не так сложно, как кажется. В этом разделе я расскажу об основной идее, на которой так или иначе основаны все алгоритмы сэмплирования. Идея такая: если равномерно выбрать точку под графиком функции плотности распределения p, то её X-координата будет взята как раз по распределению p. Это очень легко понять интуитивно: представьте себе график плотности и разбейте его на маленькие столбики, примерно так (графики сделаны в matplotlib):
Теперь видно, что когда вы берёте случайную точку под графиком, каждая X-координата будет встречаться с вероятностью, пропорциональной высоте своего столбика, т.е. как раз со значением функции плотности на этом столбике.
Таким образом, нам нужно только научиться брать случайную точку под графиком плотности нужного распределения. Как же это сделать?
Есть разные варианты этой идеи, на которых я не буду останавливаться подробно. Если вкратце, то эта идея и её вариации хорошо работают со сложными плотностями в размерности, исчисляемой единицами, но в действительно высокой размерности всё-таки начинаются сложности. Из-за эффектов проклятия размерности классические пробные распределения q получают разные неприятные свойства (например, в высокой размерности кожура апельсина занимает почти весь его объём, и, в частности, нормальное распределение тоже почти целиком сосредоточено в очень тонкой «кожуре», а вовсе не около нуля), сэмплы в нужных местах не удаётся получить, и всё дело часто проваливается. Нужны другие методы.
Алгоритм Метрополиса-Гастингса
Суть этого алгоритма основана на той же идее: мы хотим взять точку равномерно под графиком функции. Однако подход теперь другой: вместо того чтобы пытаться накрыть всё распределение «колпаком» функции q, мы будем действовать изнутри: будем строить случайное блуждание под графиком функции, переходя от одной точки к другой, и время от времени брать текущую точку блуждания в качестве сэмпла. Поскольку в данном случае это случайное блуждание является марковской цепью (т.е. его следующая точка зависит только от предыдущей, а памяти никакой нету), этот класс алгоритмов называется ещё MCMC-сэмплированием (Markov chain Monte Carlo). Чтобы доказать, что алгоритм Метрополиса-Гастингса действительно работает, нужно знать свойства марковских цепей; но мы сейчас ничего формально доказывать не собираемся, так что я просто целомудренно оставлю ссылку на вики.
Суть в том, что мы переходим в новый центр распределения, если примем очередной шаг, и получается случайное блуждание, зависящее от распределения p: мы всегда принимаем шаг, если в эту сторону функция плотности увеличивается, и иногда отвергаем, если уменьшается (отвергаем не всегда, потому что нам надо уметь выходить из локальных максимумов и блуждать под всем графиком p). Замечу, кстати, что когда шаг отвергается, мы не просто отбрасываем новую точку, а повторяем второй раз то же самое x (t) — таким образом высока вероятность повторять сэмплы вокруг локальных максимумов распределения p, что соответствует большей плотности.
И снова картинка — вот типичное блуждание на плоскости под графиком смеси двух двумерных гауссианов:
Чтобы подчеркнуть, насколько это на самом деле простой алгоритм, я приведу код, которым был порождён этот график.
Итак, мы получили случайное блуждание под графиком плотности p(x); на самом деле это ещё надо доказать, но в математику мы углубляться не будем, так что поверьте на слово. Что теперь делать с этим случайным блужданием, нам же нужны независимые сэмплы, а тут получается, что следующая точка блуждания заведомо лежит рядом с предыдущей, и никакой независимости нет и в помине?
Ответ простой: нужно брать не каждую точку, а только некоторые, отделённые друг от друга многими шагами. Поскольку это случайное блуждание, то если большая часть q сосредоточена в радиусе ε, а общий радиус, в котором сосредоточено p, равен D, то для получения независимого сэмпла нужно будет порядка шагов. В это вы, опять же, можете поверить на слово, а можете вспомнить классическую задачку из курса теории вероятностей о том, как далеко за n шагов уйдёт точка, которая с равной вероятностью двигается налево и направо; уйдёт она в среднем на , так что логично, что шагов будет квадратичное число.
А теперь главная фишка: это квадратичное число зависит от радиусов двух распределений, но при этом совершенно не зависит от размерности. Сэмплирование по методу марковских цепей Монте-Карло в гораздо меньшей степени подвержено проклятию размерности, чем другие методы, которые мы обсуждали; именно поэтому оно и стало, можно сказать, золотым стандартом. На практике, правда, D оценить трудно, так что в конкретных реализациях обычно делают так: сначала некоторое достаточно число первых шагов, скажем 1000, отбрасывают (это называется burn-in, и это действительно важно, потому что начальная точка может попасть в неудачную область p, так что перед началом процесса надо точно убедиться, что мы уже ходили достаточно долго), а потом берут каждый n-й сэмпл, где n подбирают экспериментально, исходя из реально получающейся автокорреляции в последовательности сэмплов.
Сэмплирование по Гиббсу
И последний на сегодня алгоритм сэмплирования — сэмплирование по Гиббсу. Это на самом деле частный случай алгоритма Метрополиса-Гастингса, очень популярный и простой частный случай.
Идея сэмплирования по Гиббсу ну совсем простая: предположим, что мы находимся в очень большой размерности, вектор x очень длинный, и нам сложно выбирать весь сэмпл сразу, не получается. Давайте попробуем выбирать сэмпл не весь сразу, а покомпонентно. Тогда наверняка эти одномерные распределения окажутся проще, и сэмпл мы выберем.
Формально говоря, мы пробегаем по компонентам вектора , на каждом шаге фиксируем все переменные, кроме одной, и выбираем последовательно по распределению
От общего случая блуждания по Метрополису-Гастингсу это отличается тем, что теперь мы двигаемся на каждом шаге вдоль одной из координатных осей; вот соответствующая картинка:
Сэмплирование по Гиббсу — это частный случай алгоритма Метрополиса для распределений , и вероятность принятия каждого сэмпла получается всегда равна 1 (можете это доказать в качестве упражнения). Поэтому сэмплирование по Гиббсу сходится, и, так как это такое же случайное блуждание по сути, верна та же квадратичная оценка.
Для сэмплирования по Гиббсу не нужно никаких особенных предположений или знаний. Можно быстро сделать работающую модель, и поэтому это очень популярный алгоритм. Заметим ещё, что в больших размерностях может оказаться эффективнее сэмплить по несколько переменных сразу, а не по одной — например, часто бывает, что у нас двудольный граф из переменных, в которых все переменные из одной доли связаны со всеми переменными из другой доли (ну или со многими), а между собой не связаны. В такой ситуации сам Бог велел зафиксировать все переменные одной доли и просэмплировать все переменные в другой доле одновременно (это можно понимать буквально — поскольку при такой структуре все переменные одной доли условно независимы при условии другой, их можно сэмплировать независимо и параллельно), потом зафиксировать все переменные второй доли и так далее.
Эпоха сэмплирования
Есть два громких хита «нулевых» — S.O.S. Рианны и Paper Planes M.I.A, которые вышли с разницей в год. Для Рианны S.O.S. стала еще одной победой в чартах, а Paper Planes для M.I.A — вообще главным хитом в карьере. Это их песни? Да, но нет.
Этих треков не существовало бы, если бы не мотив отсюда и гитарная партия отсюда. Воровство? Нет, сэмплирование — законная практика в музыкальной индустрии.
Объясняем, что такое сэмплы, какими они бывают и как помогают музыкантам.
Краткая история сэмплов
Сэмпл — это звуковой фрагмент трека, чаще всего пара полноценных секунд или инструментальная партия. Практику, когда сэмплы из одной песни берут для создания другой, называют сэмплированием. Так можно делать музыку не с нуля, а на базе того, что уже записано.
Начало эпохи сэмплирования — 1940-е годы. Инженер-акустик Пьер Шеффер записывал звуки окружающей среды, резал их на мелкие кусочки и монтировал как хотел. Из этих фрагментов, или сэмплов, он создавал песни (хотя, строго говоря, песнями это назвать было очень сложно). Для своих работ Шеффер даже ввел новое понятие — «конкретная музыка».
Сэмплирование в привычном понимании появилось летом 1973 года. Клайв Кэмпбелл aka DJ Kool Herс играл на тусовке сестры. У него был фирменный трюк, «карусель»: он брал две пластинки с нужными треками, выбирал в них крутые партии и сводил их. Получалась бесконечная петля, которая приводила тусовку в восторг. Поверх кто-то даже фристайлил. По сути, рождался новый трек — аранжировка из «карусели» с чьим-то речитативом.
Первым официальным треком на основе сэмпла считается The Sugarhill Gang — Rapper’s Delight 1979 года. По совместительству это еще и первая коммерчески успешная хип-хоп песня в истории музыки. В качестве сэмпла тут взяли мелодию диско-хита группы Chic — Good Times. Лидер Chic Найл Роджерс посчитал, что трек использовали незаконно, и подал в суд. Все закончилось хорошо: до самих судебных разбирательств не дошло — музыканты быстро заключили соглашение, и фронтмена Chic добавили в соавторы Rapper’s Delight.
Сэмплирование часто становится поводом для разбирательств — но только если музыканты берут фрагменты треков в качестве сэмплов, а согласия автора не спрашивают и роялти ему не платят. О том, как это бывает и к чему приводит, мы еще скажем.
Какими бывают сэмплы и зачем они нужны
У музыки есть жанры, а у сэмплов — категории. Они довольно условные, но этого хватает, чтобы обозначить характеристику и задачи применения. Сэмплы делятся на:
Музыкальные. Отрывки песен, конкретные инструментальные партии, от вокала до звона треугольника.
Голосовые. Записи разговоров — телефонных или на диктофон. К голосовым сэмплам еще относят диалоги из фильмов. В песнях и такое встречается.
Природные. Звуки природы — стук дождя, шум волн, крик чаек, трещание сверчков, шелест листвы.
Причин, по которым используют сэмплы — вагон, но основных три:
ДОПОЛНЯТЬ. Представим музыканта, у которого есть очень крутая идея для трека, но не хватает какой-то мелочи. И вот эта мелочь находится — но в другой песне.
Свежий пример — Break My Heart Дуа Липы. Трек начинается с партии бас-гитары, которая задает основу всей композиции. Эта основа — слегка переделанная мелодия одного из главных бэнгеров, Need You Tonight группы INXS.
СОЗДАВАТЬ НОВОЕ. Если говорить о создании на сэмпле с нуля, то лучше всех ситуацию объяснит трек Old Town Road рэпера Lil Nas X. Основа — фрагмент из инструменталки 33 Ghosts IV группы Nine Inch Nails. Теперь у Old Town Road 14 платиновых сертификатов в США.
Еще есть треки, которые целиком и полностью состоят из другой музыки. В 2000 году австралийцы The Avalanches выпустили альбом Since I Left You, в котором не было ни одного оригинального звука — все композиции на 100% состояли из сэмплов. The Avalanches стали пионерами субжанра «пландерфоника» — когда группа не пишет музыку сама, а собирает ее из кучи чужих сэмплов. В их треке Since I Left You — около 900 таких фрагментов.
ПОДЧЕРКИВАТЬ. Еще сэмплы используют, чтобы создать нужную атмосферу или сделать акцент на посыл. Возьмем трек Soulmate рэпера Мака Миллера. Он начинается с монолога героя Робина Уильямса из фильма «Умница Уилл Хантинг» о поиске родственной души. Эти слова передают смысл, который Миллер раскрывает в треке.
Если говорить об атмосфере, примеров будет намного больше. Один из них — Metronomy и их самый популярный альбом The English Riviera. Заглавный трек начинается с плеска волн и крика чаек. Такой ход выстраивает в голове слушателя декорации: небольшой курортный городок, где разворачивается история выяснения непростых отношений.
Сэмплы — good or evil?
У сэмплов есть и сторонники, и критики. И чаще всего в их аргументах встречаются три мнения:
Сэмплы — это хорошо. Они открыли поле для экспериментов — настолько огромное, что границ не видно. В мире постмодернизма использовать чужую музыку — нормально. Но слушателю важнее, как обыгрываются семь нот, а не как они играются.
Сэмплы — это спорно. Раньше условный сингер-сонграйтер сидел с гитарой дни напролет и, страдая, выжимал из себя материал. Сейчас все намного проще. Артист берет сэмпл, заливает его в какой-нибудь Ableton или Fruity Loops, накидывает сверху трещоток, басов, и все — новый хит готов. Да, это тоже сонграйтерство, но с готовыми фрагментами.
Сэмплы — это очень-очень плохо. В идеальном мире, чтобы получить добро на использование сэмпла, нужно отправить запрос. Если его одобрят, автор этого фрагмента музыки, его менеджмент или лейбл определятся с оплатой — одноразовой или отчислениями. В этом случае автор трека становится соавтором и получает проценты, о которых договоритесь.
Но нередко музыканты используют чужие песни без согласия их авторов.
Так было с хитом Stay With Me Сэма Смита — он продвигался в чартах и приносил Смиту прибыль. Все было хорошо до тех пор, пока легендарный музыкант Том Петти не услышал в этом треке не отголоски, а прямое совпадение со своей песней I Won’t Back Down, которую написал вместе с Джеффом Линном. Обошлось без суда — Петти и Линну предложили 12,5% авторских прав, они согласились.
Найти сэмпл в стоге сэмплов
Кажется, составить что-то из сэмплов — легко. Но на самом деле здесь куча нюансов, начиная с отбора материала и заканчивая тем, чтобы получить разрешение на использование. Но если все сделать честно и четко, результат впишется в историю музыки.
Этот эксперимент доказывает, что музыка ушла далеко за пределы записи нот в тетрадку. Сочинять — это не только перебирать аккорды до бесконечности, но и перебирать песни, пробуя сделать из них что-то новое. Главное — не забыть спросить разрешения на сэмпл.