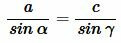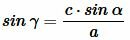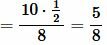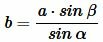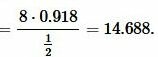Теорема синусов для чего нужна

Теорема синусов (ЕГЭ 2022)

Существуют две теоремы, свзанные с тригонометрией, которые могут оказать тебе огромную услугу в решении задач — теорема синусов и теорема косинусов.

Особенно в решении задач продвинутого уровня, за которые можно получит неплохие баллы на экзамене!

О теореме косинусов можешь прочитать пройдя по ссылке, а здесь мы поговорим про теорему синусов. Легкую и полезную.

Теорема синусов — коротко о главном

Для любого \( \displaystyle \Delta ABC\):

(здесь \( \displaystyle R\) – радиус описанной окружности)

Теорема синусов — подробнее

Что же нам сообщает теорема синусов? Вероятнее всего, что-нибудь о синусах, не правда ли? Давай сформулируем.

Первый вопрос, который возникает при взгляде на эту формулу: «Но при чём же здесь вообще \( \displaystyle R\)?».

Вот давай именно с него и начнём.

Теорема синусов. Доказательство

Тебе уже известно, что около каждого треугольника можно описать окружность. Мы это и сделаем. А потом проведём диаметр \( \displaystyle BO\).

Пусть этот диаметр пересекает окружность в точке \( \displaystyle K\). Давай рассмотрим \( \displaystyle \Delta BKC\).

Что же это за треугольник?

Ну, конечно же, прямоугольный, ведь в \( \displaystyle \Delta BKC\) угол \( \displaystyle C\) опирается на диаметр \( \displaystyle BK\quad\Rightarrow \quad\angle C=90<>^\circ \) (вспоминаем тему «Вписанный и центральный угол окружности»).

Но и кроме того, \( \displaystyle \angle K\) в \( \displaystyle \Delta BKC\) равен \( \displaystyle \angle A\) в \( \displaystyle \Delta ABC\), потому что эти углы опираются на одну дугу \( \displaystyle BC\) (опять вспоминаем ту же тему).

А теперь просто запишем выражение для синуса \( \displaystyle \angle K\) в прямоугольном \( \displaystyle \Delta BKC\) \( \displaystyle \sin \angle K=\frac\).

Но ведь \( \displaystyle BK\) – диаметр \( \displaystyle \quad\Rightarrow\quad BK=2R\), и \( \displaystyle \sin \angle K=\frac<2R>\).

Вспомним, что \( \displaystyle \angle K=\angle A\) и получим \( \displaystyle \sin \angle A=\frac<2R>\quad\Rightarrow\quad \frac<\sin \angle A>=2R\).

Вот и всё! Провели одну линию, рассмотрели один прямоугольный треугольник – и доказательство готово.

Но как же быть с углами \( \displaystyle B\) и \( \displaystyle C\)? – спросишь ты.

Да, точно также. Давай рассмотрим \( \displaystyle \angle B\).

Теперь проведём диаметр \( \displaystyle AO\) и соединим точки \( \displaystyle K\) и \( \displaystyle C\).

Как-то тут немного по-другому получается, ты заметил? \( \displaystyle \Delta AKC\), конечно, прямоугольный, так как \( \displaystyle \angle C\) опирается на диаметр \( \displaystyle AK\).

Но теперь \( \displaystyle \angle K+\angle B=180<>^\circ \), потому что четырехугольник \( \displaystyle ABCK\) – вписанный. (Надеюсь, ты ещё помнишь, что для угла \( \displaystyle A\) у нас было \( \displaystyle \angle A=\angle K\).) В чём же дело?

Ну, просто \( \displaystyle \angle B\) – тупой, поэтому и получилось такое различие. Но, к счастью, для теоремы синусов это различие не играет роли. Сейчас мы в этом убедимся.

Итак, запишем выражение для синуса \( \displaystyle \angle K\) в прямоугольном \( \displaystyle \Delta AKC\).

\( \displaystyle \sin \angle K=\frac\); то есть \( \displaystyle \sin \angle K=\frac<2R>\)

Значит, \( \displaystyle \sin \angle B=\frac<2R>\quad\Rightarrow\quad \frac<\sin \angle B>=2R\).

Ну вот, мы рассмотрели и острый, и тупой угол. Если ты все ещё беспокоишься об угле \( \displaystyle C\), то проделай все те же действия самостоятельно и убедись, что все получается.

Обрати внимание, что мы доказали «четверное равенство».

в такой последовательности:

А теперь внимание! Обсудим пользу этой теоремы

Понимаешь, теорема синусов – единственный разумный способ для нахождения радиуса описанной окружности.

Почему я так говорю? А ты вспомни сам: ну где ещё в формулах участвует \( \displaystyle R\)?! Возможно, правда, ты знаком с формулой \( \displaystyle S=\frac<4R>\), то есть \( \displaystyle R=\frac<4S>\quad\), но!

Из теоремы синусов: \( \displaystyle R=\frac<2\sin \angle A>\)

Из формулы площади: \( \displaystyle R=\frac<4S>\).

Чувствуешь разницу? В первой формуле нужно знать только одну сторону и один угол, а во второй формуле – все стороны, да ещё и площадь! Ну и какую формулу легче применить?

А кроме того, открою тебе маленький секрет: формула \( \displaystyle S=\frac<4R>\) как раз и доказывается именно с применением теоремы синусов.

Итак, теорема синусов бывает полезна и для нахождения синуса какого – то угла, если известны две стороны и один угол.

Но в основном теорема синусов – главный инструмент для нахождения радиуса описанной окружности.

Запомни это очень хорошо!

Бонус: Вебинар из нашего курса подготовки к ЕГЭ

ЕГЭ 6, 14, 16. Теорема косинусов и синусов

Универсальный инструмент при решении треугольников — это теоремы косинусов и синусов.

А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.

На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.

Источник

Теорема синусов

Доказательство теоремы синусов

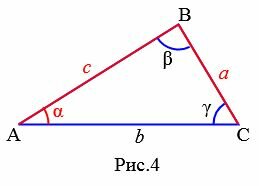
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

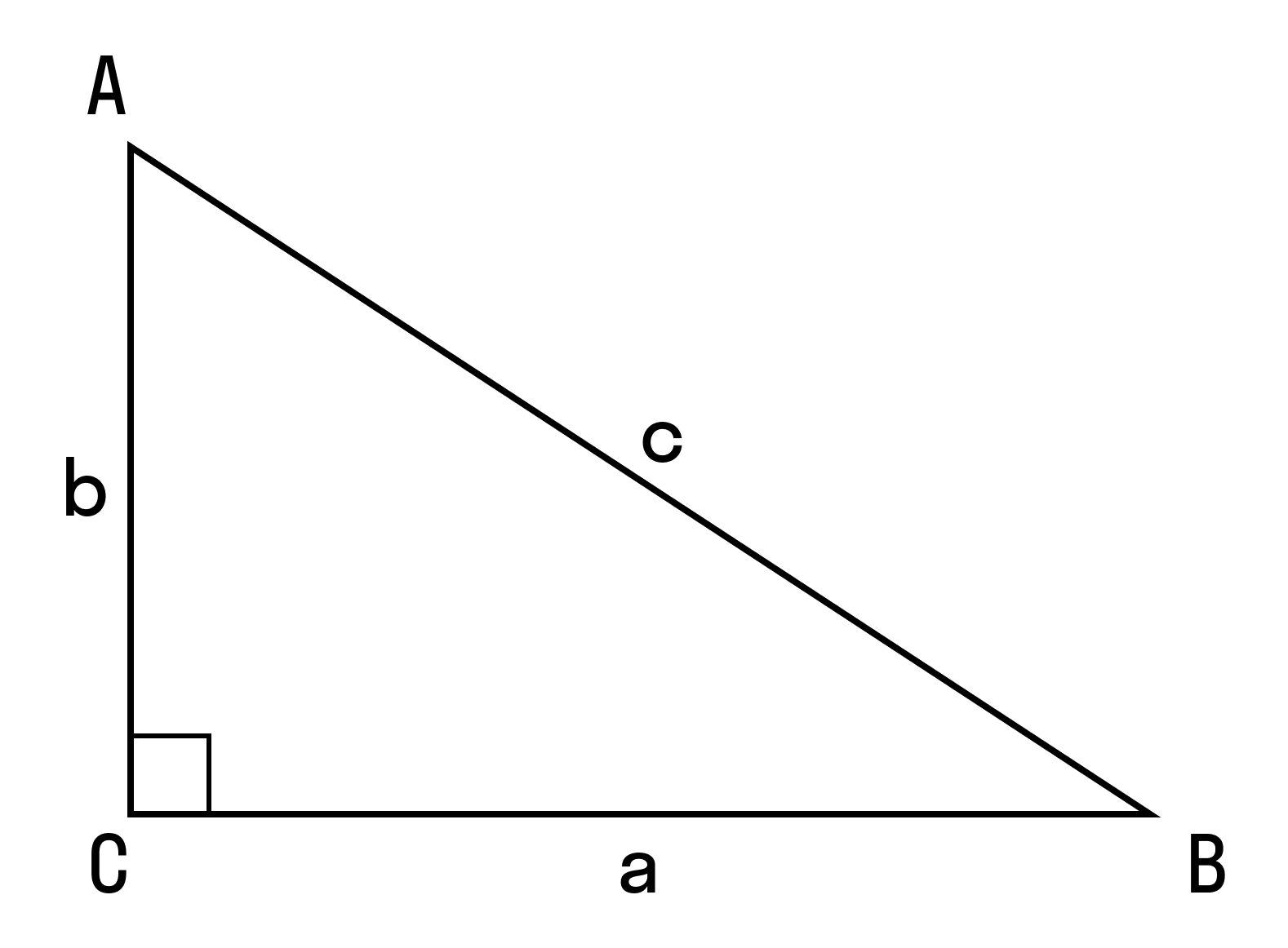
Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

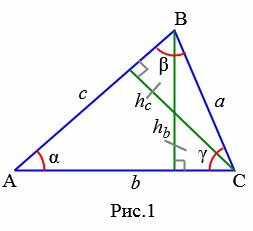
Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Вспомним свойство вписанного в окружность четырёхугольника:

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

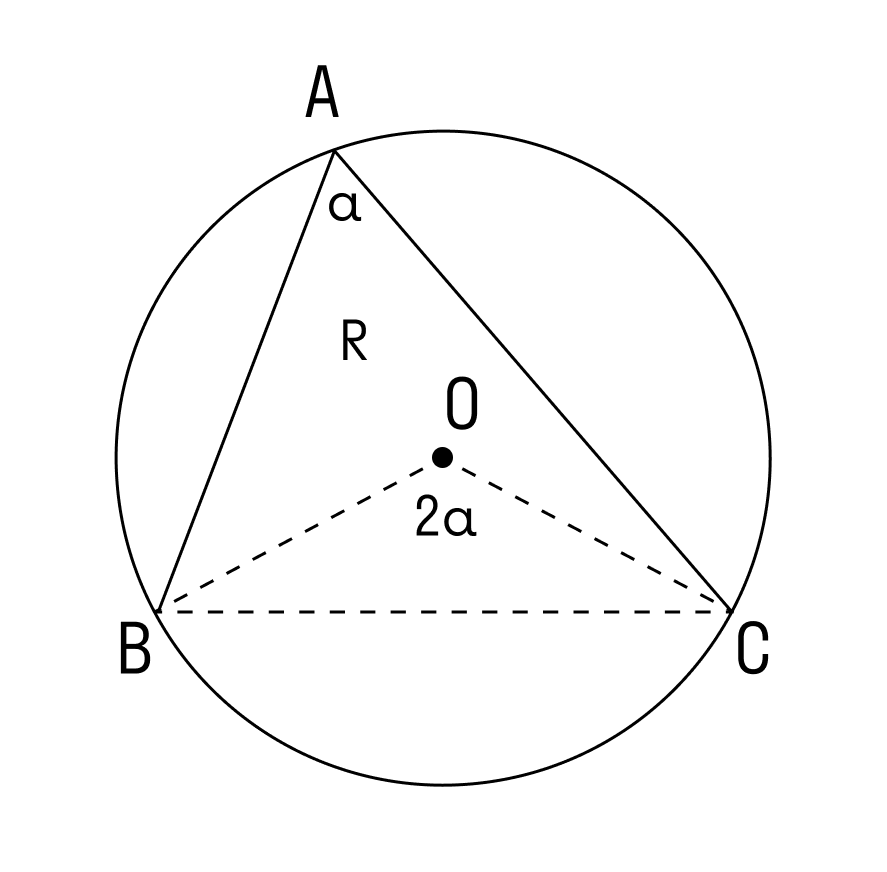
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

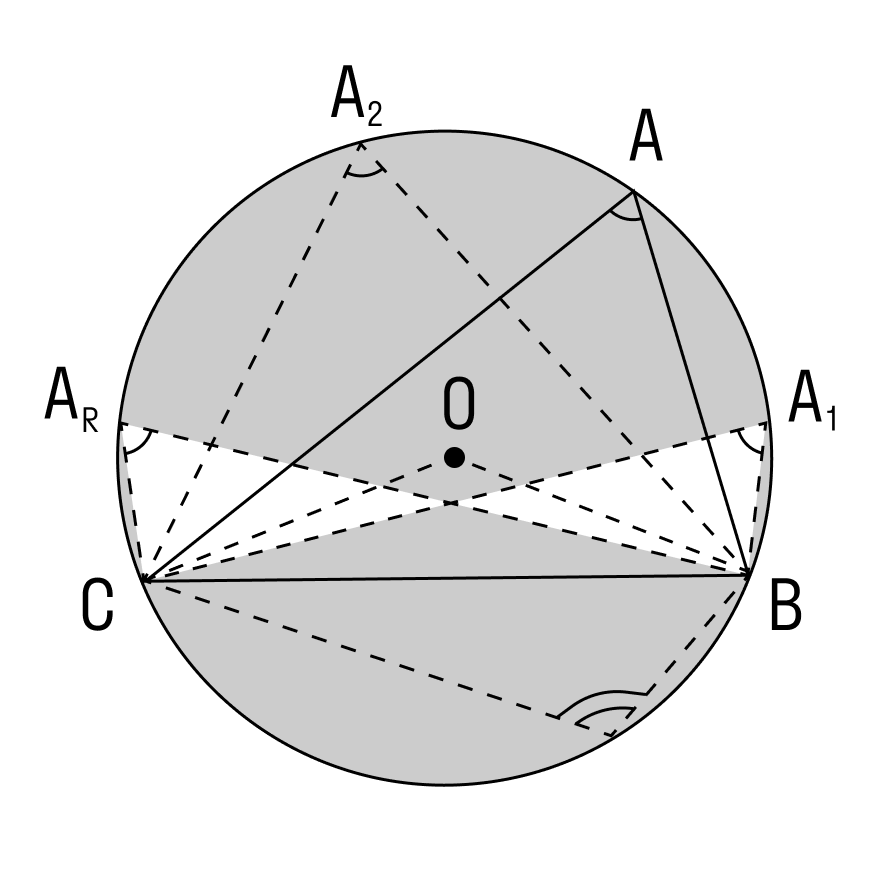
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

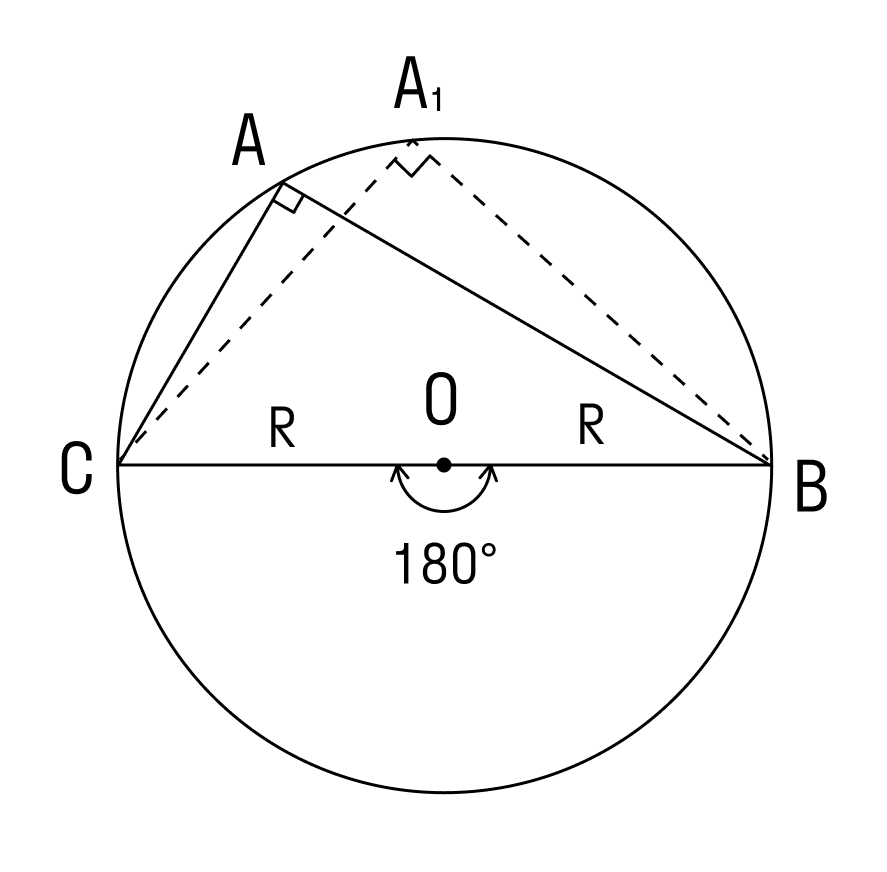
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

Источник

Теорема косинусов и синусов

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

К полученному выражению прибавим и отнимем квадрат второго катета:

Но так как b = c * cos α, то

Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

Приравниваем правые части уравнений:

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

Таким образом, теорема косинусов обобщает теорему Пифагора. Закон косинуса может быть использован для любого вида треугольника.

Описание формулы косинуса угла из теоремы косинусов

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Источник

Теорема синусов для треугольника: формула и задачи

В данной публикации мы рассмотрим одну из главных теорем евклидовой геометрии, теорему синусов, которая определяет соотношение сторон в треугольнике, а также, научимся применять ее на практике для решения задач.

Формулировка и формула теоремы

1. Обычная теорема

Стороны треугольника пропорциональны синусам противолежащих углов.

2. Расширенная теорема

В произвольном треугольнике справедливо следующее соотношение:

R – радиус описанной вокруг треугольника окружности.

Примеры задач

Задание 1
В треугольнике известна длина основания – 10 см, противолежащий основанию угол – 90°, а также, один из углов, прилегающих к нему – 45°. Найдите сторону напротив угла 45°.

Решение:
Примем неизвестную сторону за x и применим теорему синусов:

Задание 2
Гипотенуза и один из катетов прямоугольного треугольника равны, соответственно, 10 и 8 см. Найти угол, расположенный напротив данного катета.

Решение:
Как мы знаем, в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. С учетом этого, соотношение сторон выглядит следующим образом:

Значит x = arcsin (4/5) ≈ 53,1°.

Источник

Теорема синусов. Доказательство

Теорема 1 (теорема синусов). Стороны треугольника пропорциональны синусам противолежащих углов:

Доказательство. Пусть задан треугольник ABC. Проведем высоту h_b из вершины B на сторону b (Рис.1).

Из определения синуса (см. страницу Синус и косинус. Онлайн калькулятор) следует, что синус угла α равен h_b если предполагать, что c=1. Но поскольку c может иметь любое значение, то имеем

Аналогично можем записать:

Далее, для высоты h_c, опущенной из вершины C на сторону c, имеем:

, .

Теорема 2 (расширенная теорема синусов). Для произвольного треугольника справедливо следующее равенство:

где a, b, c стороны треугольника, а α, β, γ противолежащие им углы, соответственно, R− радиус описанной около треугольника окружности.

Доказательство. Пусть задан треугольник ABC и описанная окружность с радиусом R, проходящей через вершины треугольника.

В теореме 1 мы доказали справедливость равенства (a). Для доказательства (b) достаточно показать, что

Проведем через вершину C диаметр CD описанной окружности и соединим точки D и B.

1. Пусть точки D и A лежат по одну сторону от BC (Рис.2). Полученный треугольник BCD являестся прямоугольным треугольником с прямым углом B, поскольку его одна сторона совпадает с диаметром окружности. А для этого прямоугольного треугольника справедливо равенство:

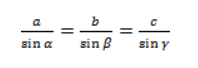
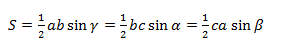
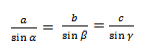
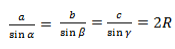
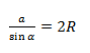
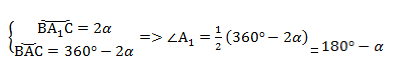
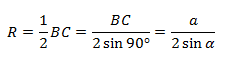
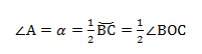
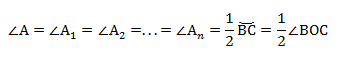
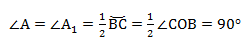
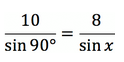
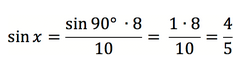
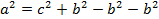
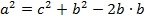
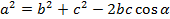
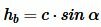
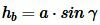
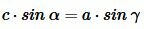
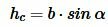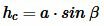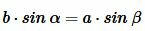
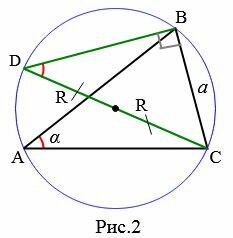
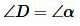Но поскольку обе эти углы опираются на дугу BC. Отсюда следует справедливость равенства (3).

2. Пусть точки D и A лежат в разные стороны от BC (Рис.3).

Поскольку BCD прямоугольный треугольник, то справедливо следующее равенство:

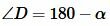Покажем, что . Действительно. Так как вписанный угол измеряется половиной дуги, на которой он упирается, то имеем:

, .

(5)

Тогда из (5) и (6) получим:

.

.

(7)

Учитывая (7), уравнение (4) можно записать так:

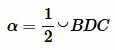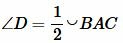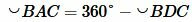
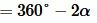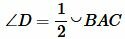
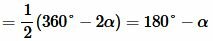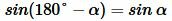Но . Тогда из (8) получим равенство (3).

Примеры и решения

Задание 1. В треугольнике ABC a=8, c=10, угол α=30°. Найти сторону b (Рис.4).

Решение. Из теоремы синусов, имеем:

Поскольку сумма всех углов треугольника равна 180°, то β=180°−30°−36.68°=113.32°.

Далее, из теоремы синусов:

Задание 2. В треугольнике ABC c=16, α=30°, β=45°. Найти стороны a, b (Рис.5).

Источник