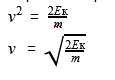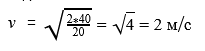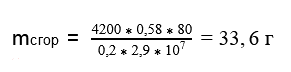закон сохранения внутренней энергии для изолированной системы гласит что

Закон сохранения энергии для механических процессов

Одним из наиболее фундаментальных законов природы является закон сохранения энергии, согласно которому важнейшая физическая величина – энергия – сохраняется в изолированной системе.

Закон сохранения энергии: в изолированной системе энергия может переходить из одной формы в другую, но ее количество оста­ется постоянным.

Если система не изолирована, то ее энергия может изменяться либо при одновременном изменении энергии окружающих тел на такую же величину, либо за счет изменения энергии взаимодействия тела с окружающими телами. При переходе системы из одного состояния в другое изменение энергии не зависит от того, каким способом (в результате каких взаимодействий) происходит переход, т.е. энергия – однозначная функция состояния системы.

Закон сохранения энергии является строгим законом природы, справедливым для всех известных взаимодействий. Согласно известной теории Э. Нётер, он связан с однородностью времени, т.е. с тем фактом, что все моменты времени эквивалентны и физические законы не меняются со временем.

Закон сохранения энергии для механических процессов был установлен Г. Лейбницем (1686) а для немеханических – в середине XIX в. Ю.Р. Майером (1845), Дж. Джоулем и Г. Гельмгольцем (1847).

В термодинамике закон сохранения энергии называется первым началом термодинамики.

Открытие закона сохранения и превращения энергии вначале было итогом развития механики. Но затем, благодаря дальнейшим экспериментальным исследованиям и теоретическому осмыслива­нию их результатов, становилось ясно, что содержание этого закона значительно глубже, что он – всеобщий закон природы. Это позволило быстрыми темпами развивать теорию тепловых процессов, что привело к появлению термодинамики. Особо важную роль закон сохранения и превращения энергии сыграл в изучении электрических и магнитных явлений, своеобразие и специфика которых не допускали применения других механических (по своему происхождению) понятий.

Становление и утверждение закона сохранения энергии охватывает длительный период – более полутораста лет. Как уже указыва­лось, первым был установлен закон сохранения энергии для меха­нического движения.

Первый период был связан с длительной дискуссией о так на­зываемых «мерах движения» и введением понятия «работа».

По Лейбницу, основной закон природы состоит не в сохранении количества движения, но в том, что необходимо сохранить одно и то же количество двигательной деятельности, которое означает совсем не то, что понимают сторонники Декарта под количеством движения.

Это произведение mv 2 он и выбрал в качестве меры движения. «Живая сила» (mv 2 ), по мнению Лейбница, выражает то «количество двигательной деятельности, которое сохраняется в природе».

Теперь мы знаем, что mv 2 есть удвоенная кинетическая энергия движущегося тела. Таким образом, Лейбниц, по сути, вначале сформулировал закон сохранения кинетической энергии. Кинетическая энергия, по современной терминологии, определяется как физическая величина, равная половине произведения массы частицы на квадрат ее скорости: . Это уже знакомая «живая сила» Лейбница, только разделенная пополам. Разделить ее на два предложил французский механик Г. Кориолис.

Основанием послужила теорема, доказанная за несколько лет до этого французским математиком Л.Н. Карно. Согласно его теореме, если тело движется под действием постоянной силы, то удвоенное произведение силы (F) на перемещение (s) равно разности «живых сил» в конце и начале перемещения:

.

Тогда это было новым словом в практической механике.

Произведение силы на перемещение в формуле (2.1) Г. Кориолис вслед за другим французским механиком, Ж.В. Понселе, назвал работой. Если работу обозначить через А и записать как

то формулу следует переписать в виде:

.

Появившиеся в знаменателях этой формулы двойки дали основание Г. Кориолису принять за меру движения половину лейбницевой «живой силы».

Теорему, выраженную формулой, принято называть теоремой о кинетической энергии. В соответствии с ней работа сил, действующих на тело, равна изменению кинетической энергии этого тела:

Из теоремы следует, что кинетическая энергия равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему заданную скорость движения.

Следующий важный шаг в развитии понятия механической энергии был сделан Г. Гельмгольцем, чей вклад в обоснование закона сохранения энергии будет более подробно рассмотрен ниже. Изучая движение тел под действием сил, которые постоянны или зависят от расстояния, но не от времени и скорости, он обратил внимание на то, что левую часть уравнения в таком случае всегда можно представить в виде разности значений некоторой величины, характеризующей взаимодействие рассматриваемых тел.

Поскольку новая величина имела такую же размерность, что и «живая сила», Г. Гельмгольц предложил и ее назвать «силой», но не «живой», а «напряженной». Впоследствии «напряженная сила» Гельмгольца была переименована в потенциальную энергию. Потенциальная энергия – это энергия взаимодействия. Она определяется работой, которую должны совершить силы, чтобы переместить тело из данного положения в нулевое:

Выбор нулевого положения произволен. Поэтому потенциальная энергия определена неоднозначно: по отношению к разным нулевым уровням потенциальная энергия одного и того же тела будет различной. Например, потенциальная энергия тела, взаимодействующего с Землей, может быть найдена по формуле Е_П = mgh, где h — высота центра тяжести тела, отсчитываемая от нулевого уровня. Принимая за нулевой уровень поверхность Земли, пола в комнате или, наконец, стола, над которым находится рассматриваемое тело, мы получим разные значения h и соответственно разные значения потенциальной энергии.

Для потенциальной энергии справедлива теорема, аналогичная теореме о кинетической энергии. По теореме о потенциальной энергии, работа консервативных сил при любом движении тела равна разности потенциальных энергий в начальном и конечном состояниях:

Рассматривая консервативные системы, т.е. системы, в которых действуют лишь консервативные силы, Гельмгольц пришел к выводу, что одна и та же величина может быть выражена и через прира­щение кинетической энергии системы, и через убыль ее потенци­альной энергии. Это означает, что увеличение кинетической энер­гии рассматриваемой системы всегда сопровождается соответст­вующим уменьшением ее потенциальной энергии, и наоборот:

.

Если переписать равенство в виде

,

то станет ясно, что сумма кинетической и потенциальной энергий рассматриваемой системы в процессе ее движения не меняется. На основании этого можно объединить обе величины в одну — полную механическую энергию системы:

Из отношения следует, что Е = const.

Итак, при любых процессах, происходящих в консервативной системе, ее полная механическая энергия остается неизменной. Это утверждение называется законом сохранения механической энергии.

Поскольку кинетическую энергию Г. Гельмгольц называл «живой силой», а потенциальную энергию – «напряженной», то первая формулировка закона сохранения энергии, данная Гельмгольцем, такова:

Когда тела природы действуют друг на друга с силами притяжения или отталкивания, не зависимыми от времени и скорости, то сумма живых сил и напряженных сил остается постоянной.

Следующий этап установления закона сохранения и превращения энергии связан с изучением превращения различных форм энергии друг в друга.

На начальном этапе изучения превращения различных форм движения друг в друга исключительную роль сыграл С. Карно, который впервые занялся изучением вопроса превращения теплоты в работу паровых машин.

Поставив вначале достаточно скромную техническую задачу, как наиболее экономно использовать топливо в паровых машинах, он решил не только эту проблему, но и получил целый ряд принципи­ально новых результатов, имеющих важное значение для развития многих направлений естествознания.

Во-первых, С. Карно нашел наиболее оптимальные условия рабо­ты тепловой машины (цикл Карно), при которых можно добиться максимального коэффициента ее полезного действия. Теорема Карно о максимальном коэффициенте полезного действия тепловых машин сыграла в дальнейшем важную роль в установлении одного из фун­даментальных законов природы — второго начала термодинамики.

Затем, продолжая свои исследования, он пришел к правильным взглядам на природу теплоты, как на совокупность механического движения атомов, из которых состоят физические тела.

Он отмечал: Тепло – не что иное, как движущая сила или, вернее, как движение, из­менившее свой вид, – это движение частиц тела,- повсюду, где происходит уничтожение движущей силы, возникает одновременно теплота в количест­ве, пропорциональном количеству исчезнувшей движущей силы. Обратно: всегда при исчезновении тепла возникает движущая сила. Таким образом, можно высказать общее положение: движущаяся сила существует в природе в неизменном количестве; она, собственно говоря, никогда не создается, никогда не уничтожается; в действительности она меняет форму, т.е. вызы­вает то один род движения, то другой, но никогда не исчезает.

Как видно из приведенной цитаты, С. Карно сформулировал за­кон сохранения и превращения «сил» (по современной терминологии – энергии), закон сохранения и превращения тепловой и механической энергии. Он даже впервые приблизительно определил механический эквивалент теплоты.

По некоторым представлениям, которые у меня сложились относитель­но теории теплоты, – писал Карно, – создание единицы движущей силы(по современной терминологии – единицы механической работы) требует затраты 2,7 единицы тепла.

При переводе в современные единицы это значение механиче­ского эквивалента равно примерно 370 кГм/ккал.

Противоположную С. Карно задачу, а именно: исследование об­ратного процесса превращения работы в тепло в результате трения, поставил себе Б. Томпсон. Работая на пушечных заво­дах, он заметил, что при сверлении пушечных стволов они очень сильно нагреваются.

Источник

Закон сохранения механической энергии

Энергия: что это такое

Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.

Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.

Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.

Механическая энергия

Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.

Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.

Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.

Кинетическая энергия

Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.

Кинетическая энергия

Ек = (m*v^2)/2

Ек — кинетическая энергия [Дж]

Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.

Задачка раз

Определить кинетическую энергию собаченьки массой 10 килограмм, если она бежала за мячом с постоянной скоростью 2 м/с.

Решение:

Формула кинетической энергии Ек = (m*v^2)/2

Ответ: кинетическая энергия пёсы равна 20 Дж.

Задачка два

Найти скорость бегущего по опушке гнома, если его масса равна 20 килограммам, а его кинетическая энергия — 40 Дж

Решение:

Формула кинетической энергии Ек = (m*v^2)/2

Ответ: гном бежал со скоростью 2 м/с.

Потенциальная энергия

В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.

Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.

Потенциальная энергия деформированной пружины

Еп — потенциальная энергия [Дж]

x — удлинение пружины [м]

Потенциальная энергия

Еп = mgh

Еп — потенциальная энергия [Дж]

g — ускорение свободного падения [м/с^2]

На планете Земля g ≃ 9,8 м/с^2

Задачка раз

Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с^2.

Решение:

Формула потенциальной энергии Еп = mgh

Eп = 0,1 * 9,8 * 2500=2450 Дж

Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.

Задачка два

Найти высоту горки, с которой собирается скатиться лыжник массой 65 килограмм, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с^2.

Решение:

Формула потенциальной энергии Еп = mgh

Переведем 637 кДж в Джоули.

637 кДж = 637000 Дж

h = 637 000/(65 * 9,8) = 1000 м

Ответ: высота горы равна 1000 метров.

Задачка три

Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:

Потенциальная энергия вычисляется по формуле: E = mgh

Таким образом, получим, что

Ответ: E1 = E2.

Закон сохранения энергии

В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.

Закон сохранения энергии

Полная механическая энергия замкнутой системы остается постоянной.

Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:

Закон сохранения энергии

Еполн.мех. = Еп + Eк = const

Еполн.мех. — полная механическая энергия системы [Дж]

Еп — потенциальная энергия [Дж]

Ек — кинетическая энергия [Дж]

const — постоянная величина

Задачка раз

Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?

Решение:

Должен выполняться закон сохранения энергии:

В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна.

В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.

Это можно описать соотношением:

Еп1 + Ек1 = Еп2 + Ек2

Разделим на массу левую и правую часть

Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.

Ответ: высота увеличится в 4 раза

Задачка два

Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?

Решение

По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0.

Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0.

Ответ: Емех = mgh0.

Задачка три

Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.

Решение:

Переведем массу из граммов в килограммы:

У поверхности земли полная механическая энергия мяча равна его кинетической энергии:

Е = Ек0 = (m*v^2)/2 = (0,1*6^2)/2 = 1,8 Дж

На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:

mgh = E — (m*v^2)/2 = 1,8 — (0,1 * 2^2)/2 = 1,6 Дж

h = E/mg = 1,6/0,1*10 = 1,6 м

Ответ: мяч имел скорость 2 м/с на высоте 1,6 м

Переход механической энергии во внутреннюю

Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.

Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.

Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.

Задачка

Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?

Решение:

В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.

В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2

Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр

Емех = Емех/2 + Евнутр

Ответ: во внутреннюю перейдет половина начальной кинетической энергии

Закон сохранения энергии в тепловых процессах

Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.

Вот что сформулировал Фурье:

При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.

Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.

Дальше Карно установил, что тепловую энергию, которой обладает на­гретое тело, непосредственно невозможно превратить в механиче­скую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.

Закон сохранения энергии в тепловых процессах

При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.

Математически его можно описать так:

Уравнение теплового баланса

Q отд = Q пол

Qотд — отданное системой количество теплоты [Дж]

Q пол — полученное системой количество теплоты [Дж]

Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:

Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.

Задачка раз

Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.

Удельная теплота сгорания спирта 2,9·10^7Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С).

Решение:

При нагревании тело получает количество теплоты

где c — удельная теплоемкость вещества

При сгорании тела выделяется энергия

где q — удельная теплота сгорания топлива

По условию задачи нам известно, что на нагревание пошло 20% затраченной энергии.

Ответ: масса сгоревшего топливаа равна 33,6 г.

Задачка два

Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг*℃, удельная теплота плавления льда равна 3,3*10^5 Дж/кг.

Решение:

Для нагревания льда до температуры плавления необходимо:

Qнагрев = 2100 * 0,5 * (10-0) = 10500 Дж

Для превращения льда в воду:

Qпл = 3,3 * 10^5 * 0,5 = 165000 Дж

Q = Qнагрев + Qпл = 10500 + 165000 = 175500 Дж = 175,5 кДж

Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.

Источник

Первый закон термодинамики = Закон сохранения энергии, внутренняя энергия, тепло, работа, энтальпия, энтропия.

Первый закон термодинамики = Закон сохранения энергии гласит, (4 разные формулировки) что :

Внутрення энергия (в термодинамике) включает :

Первый закон является основой для термодинамической науки и инженерного анализа.

Базируется на возможных типах обмена (энергии), ниже приведены 3 типа систем:

Первый закон термодинамики помогает использовать ключевые концепции внутренней энергии (internal energy), тепла (heat), и работы системы (system work). которые широко используются в описании тепловых систем (heat engines).

Изменение внутренней энергии системы равно теплу (добавленному системе) минус работа, совершенная системой

1й закон не дает информации о характере процесса и не определяет конечного состояния равновесия. Интуитивно мы понимаем, что энергия переходит от объекта с более высокой температурой к объекту с менее высокой температурой. Таким образом, 2й закон нам нужен для получения информации о характере процесса.

Энтропия.

Энтропия (обычно обозначается S), функция состояния термодинамической системы, изменение которой dS в равновесном процессе равно отношению количества теплоты dQ, сообщенного системе или отведенного от нее, к термодинамической температуре Т системы.

в символьном виде записывается, как

Неравновесные процессы в изолированной системе сопровождаются ростом энтропии, они приближают систему к состоянию равновесия, в котором S максимальна (закон неубывания энтропии). Для вселенной в целом энтропия возрастает.

Источник